
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.

(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.
【答案】30°;见解析.
【解析】
试题分析:根据∠ACB和∠B的度数得出∠CAB的度数,根据角平分线的性质得出∠CAD的度数;根据∠ACD+∠ECD=180°,∠ACD=90°得出∠ACD=∠ECD=90°,证明△ACD和△ECD全等,从而得出结论.
试题解析:(1)∵在Rt△ABC中,∠ACB=90°,∠B=30°, ∴∠CAB=60°.
又∵AD平分∠CAB, ∴∠CAD=![]() ∠CAB=30°,即∠CAD=30°;
∠CAB=30°,即∠CAD=30°;
(2)证明:∵∠ACD+∠ECD=180°,且∠ACD=90°, ∴∠ECD=90°, ∴∠ACD=∠ECD.
在△ACD与△ECD中,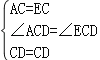 , ∴△ACD≌△ECD(SAS), ∴DA=DE.
, ∴△ACD≌△ECD(SAS), ∴DA=DE.


科目:初中数学 来源: 题型:
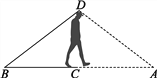
【题目】如图所示,小明为了测量河的宽度,他先站在河边的C点面向河对岸,压低帽檐使目光正好落在河对岸的A点,然后姿态不变原地转了一个角度,正好看见了他所在的岸上的一块石头B点,他发现看到B点和A点的视角相等,并测量BC=30m.你能猜出河有多宽吗?说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABE≌△ACD,且AB=AC.
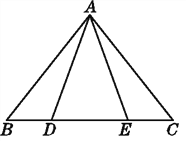
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com