
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图像经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图像经过点D、E,且tan∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图像与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
【答案】
(1)
解:∵点E(4,n)在边AB上,
∴OA=4,
在Rt△AOB中,∵tan∠BOA= ![]() ,
,
∴AB=OA×tan∠BOA=4× ![]() =2
=2
(2)
解:根据(1),可得点B的坐标为(4,2),
∵点D为OB的中点,
∴点D(2,1)
∴ ![]() =1,
=1,
解得k=2,
∴反比例函数解析式为y= ![]() ,
,
又∵点E(4,n)在反比例函数图像上,
∴ ![]() =n,
=n,
解得n= ![]()
(3)
解:如图,
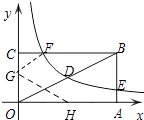
设点F(a,2),
∵反比例函数的图像与矩形的边BC交于点F,
∴ ![]() =2,
=2,
解得a=1,
∴CF=1,
连接FG,设OG=t,则OG=FG=t,CG=2﹣t,
在Rt△CGF中,GF2=CF2+CG2,
即t2=(2﹣t)2+12,
解得t= ![]() ,
,
∴OG=t= ![]() .
.
【解析】(1)根据点E的纵坐标判断出OA=4,再根据tan∠BOA= ![]() 即可求出AB的长度;(2)根据(1)求出点B的坐标,再根据点D是OB的中点求出点D的坐标,然后利用待定系数法求函数解析式求出反比例函数解析式,再把点E的坐标代入进行计算即可求出n的值;(3)先利用反比例函数解析式求出点F的坐标,从而得到CF的长度,连接FG,根据折叠的性质可得FG=OG,然后用OG表示出CG的长度,再利用勾股定理列式计算即可求出OG的长度.
即可求出AB的长度;(2)根据(1)求出点B的坐标,再根据点D是OB的中点求出点D的坐标,然后利用待定系数法求函数解析式求出反比例函数解析式,再把点E的坐标代入进行计算即可求出n的值;(3)先利用反比例函数解析式求出点F的坐标,从而得到CF的长度,连接FG,根据折叠的性质可得FG=OG,然后用OG表示出CG的长度,再利用勾股定理列式计算即可求出OG的长度.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
分数(单位:分) | 105 | 130 | 140 | 150 |
人数(单位:人) | 2 | 4 | 3 | 1 |
下列说法中,不正确的是( )
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( ) 
A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条笔直的公路AB,CD相交于点O,∠AOC为30°,指挥中心M设在OA路段上,与O地的距离为22千米.一次行动中,王警官带队从O地出发,沿OC方向行进,王警官与指挥中心均配有对讲机,两部对讲机只能在10千米之内进行通话,通过计算判断王警官在行进过程中能否与指挥中心用对讲机通话.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅共有10名员工,所有员工工资的情况如下表:
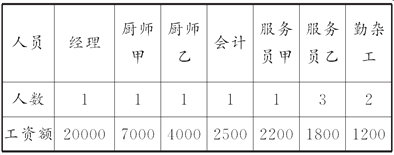
请解答下列问题:
(1)餐厅所有员工的平均工资是多少?
(2)所有员工工资的中位数是多少?
(3)用平均数还是中位数描述该餐厅员工工资的一般水平比较恰当?
(4)去掉经理和厨师甲的工资后,其他员工的平均工资是多少?它是否能反映餐厅员工工资的一般水平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com