
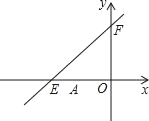
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
试题(1)将点E坐标(-8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(-6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为![]() 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,
∴k=![]() ;
;
(2)∵k=![]() ,
,
∴直线的解析式为:y=![]() x+6,
x+6,
∵P点在y=![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),
x+6),
∴△OPA以OA为底的边上的高是|![]() x+6|,
x+6|,
当点P在第二象限时,|![]() x+6|=
x+6|=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6.
∴S=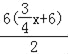 =
=![]() x+18.
x+18.
∵P点在第二象限,
∴﹣8<x<0;
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,
,
解得|n|=![]() ,
,
则n1=![]() 或者n2=﹣
或者n2=﹣![]() (舍去),
(舍去),
当n=![]() 时,
时,![]() =
=![]() m+6,
m+6,
则m=﹣![]() ,
,
故P(﹣![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
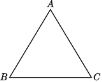
【题目】如图的等边三角形ABC是学校的一块空地,为美化校园,决定把这块空地分为全等的三部分,分别种植不同的花草.现有两种划分方案:(1)分为三个全等的三角形;(2)分为三个全等的四边形.你认为这两种方案能实现吗?若能,画图说明你的划分方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 ![]() (k≠0)在第一象限内的图像经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图像经过点D、E,且tan∠BOA= ![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图像与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
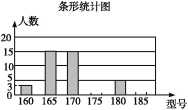
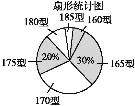
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图像. 
(1)请直接写出甲离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(2)当它们行驶4.5小时后离各自出发点的距离相等,求乙车离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,甲、乙两车从各自出发地驶出后经过多少时间相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c (a≠0)(a≠0,a,b,C为常数)的图象,若关于x的一元二次方程ax2+bx+c=m有实数根,则m的取值范围是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com