【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
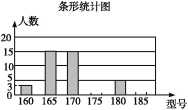
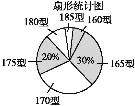
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
【答案】（1）该班共有50名学生，其中穿175型校服的学生有10名.（2）补图见解析；（3）14.4°.（4）170.
【解析】
本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键，条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．除此之外，本题也考查了中位数、众数的知识．
（1）根据穿165型的人数与其所占的百分比列式进行计算即可求出学生总人数，再乘175型所占的百分比计算即可得解．
（2）求出185型的人数，然后补全统计图即可．
（3）用185型的人数所占的百分比乘360°计算即可得解．
（4）根据众数的定义以及中位数的定义解答即可．
亮点激活精编提优100分大试卷系列答案科目：初中数学 来源： 题型：
【题目】如图，将长方形ABCD对折，得折痕PQ，展开后再沿MN翻折，使点C恰好落在折痕PQ上的点C′处，点D落在D′处，其中M是BC的中点且MN与折痕PQ交于F.连接AC′，BC′，则图中共有等腰三角形的个数是( )
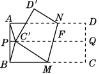
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若样本x1+1，x2+1，…，xn+1的平均数为10，方差为2，则对于样本x1+2，x2+2，…，xn+2，下列结论正确的是（ ）
A. 平均数为10，方差为2 B. 平均数为11，方差为3
C. 平均数为11，方差为2 D. 平均数为12，方差为4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与
轴、
轴分别交于点
，
．点的坐标为（
，0），点
的坐标为（
，0）．
（1）求
的值；
（2）若点
（，）是第二象限内的直线上的一个动点．当点运动过程中，试写出
的面积
与的函数关系式，并写出自变量的取值范围；
（3）探究：当运动到什么位置时，的面积为
，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为开展体育大课间活动，需要购买篮球与足球若干个．已知购买2个篮球和3个足球共需要380元；购买4个篮球和5个足球共需要700元．
(1)求购买一个篮球、一个足球各需多少元；
(2)若体育老师带了8000元去购买这种篮球与足球共100个．由于数量较多，店主给出“一律打九折”的优惠价，那么他最多能购买多少个篮球？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小区居民利用“健步行APP”开展健步走活动，为了解居民的健步走情况，小文同学调查了部分居民某天行走的步数
单位：千步
，并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图．
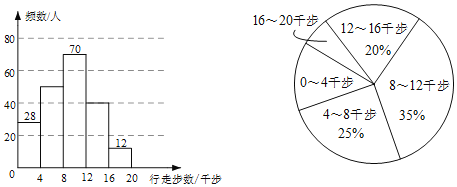
有下面四个推断：
小文此次一共调查了200位小区居民；
行走步数为
千步的人数超过调查总人数的一半；
行走步数为
千步的人数为50人；
行走步数为
千步的扇形圆心角是
．
根据统计图提供的信息，上述推断合理的是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．
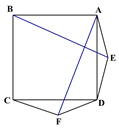
（图1） （图2） （备用图）
（1）请判断：AF与BE的数量关系是_____________，位置关系______________；
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；
（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
