
【题目】如图,在正方形ABCD中,OE=OF.求证:△AOE≌△BOF,AE⊥BF. 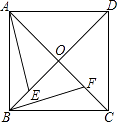
【答案】证明:∵四边形ABCD为正方形, ∴OA=OB,∠AOE=∠BOF;
在△AOE与△BOF中,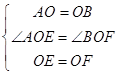 ,
,
∴△AOE≌△BOF(SAS),
延长AE交BF于点G;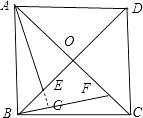
∵△AOE≌△BOF,
∴∠AEO=∠OFG,即∠AEO=∠AFG.
∵AO⊥EO,
∴∠EAO+∠AEO=90°,
∴∠GAF+∠AFG=90°,
∴AE⊥BF.
∴△AOE≌△BOF,AE⊥BF.
【解析】利用正方形的性质可得AO=BO,∠AOE=∠BOF,又OE=OF,可证明△AOE≌△BOF,得到AE=BF,延长AE交BF于点G,证明∠AEO=∠AFG.证明∠GAF+∠AFG=90°,即可解决问题.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
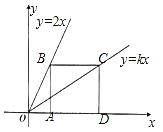
【题目】如图,点B、C分别在直线y=2x和y=kx上,点A、D是x轴上的两点,且四边形ABCD是正方形.
(1)若正方形ABCD的边长为2,则点B、C的坐标分别为 .
(2)若正方形ABCD的边长为a,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() (x>0)的图像交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图像交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.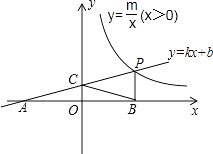
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图像上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,后解答: ![]() =
= ![]() =
= ![]() =3+
=3+ ![]()
像上述解题过程中, ![]() ﹣
﹣ ![]() 与
与 ![]() +
+ ![]() 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)![]() 的有理化因式是;
的有理化因式是; ![]() +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: ![]() =;
=; ![]() = .
= .
(3)已知a= ![]() ,b=2﹣
,b=2﹣ ![]() ,比较a与b的大小关系.
,比较a与b的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[动手操作] 如图所示,地面全是用正三角形的材料铺设而成的.
(1)用这种形状的材料为什么能铺成平整、无缝隙的地面?
(2)像上面那样铺地砖,能否全用正十边形的材料?为什么?
(3)你能不能另外想出用一种相同的正多边形材料铺地面的方案?并画出草图.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校运动会需购买A,B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.
(1)求A、B两种奖品的单价各是多少元?
(2)学校计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.求出自变量m的取值范围,并确定最少费用W的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
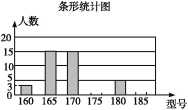
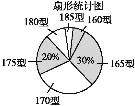
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是( )

A. ①③④ B. ②③④ C. ①②③ D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com