【题目】如图，在Rt△AEB和Rt△AFC中，BE与AC相交于点M，与CF相交于点D，AB与CF相交于N，∠E＝∠F＝90°，∠EAC＝∠FAB，AE＝AF.给出下列结论：①∠B＝∠C；②CD＝DN；③BE＝CF；④△ACN≌△ABM.其中正确的结论是( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
高中必刷题系列答案科目：初中数学 来源： 题型：
【题目】某校为开展体育大课间活动，需要购买篮球与足球若干个．已知购买2个篮球和3个足球共需要380元；购买4个篮球和5个足球共需要700元．
(1)求购买一个篮球、一个足球各需多少元；
(2)若体育老师带了8000元去购买这种篮球与足球共100个．由于数量较多，店主给出“一律打九折”的优惠价，那么他最多能购买多少个篮球？
查看答案和解析>>
科目：初中数学 来源： 题型：
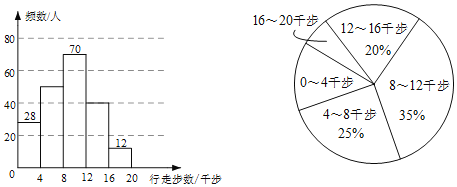
【题目】某小区居民利用“健步行APP”开展健步走活动，为了解居民的健步走情况，小文同学调查了部分居民某天行走的步数
单位：千步
，并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图．
有下面四个推断：
小文此次一共调查了200位小区居民；
行走步数为
千步的人数超过调查总人数的一半；
行走步数为
千步的人数为50人；
行走步数为
千步的扇形圆心角是
．
根据统计图提供的信息，上述推断合理的是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
中，AD是
的平分线，
，垂足为E，作
，交直线AE于点
设
，
．
若
，
，依题意补全图1，并直接写出
的度数；
如图2，若
是钝角，求的度数
用含
，
的式子表示
；
如图3，若
，直接写出的度数用含，的式子表示．
查看答案和解析>>
科目：初中数学 来源： 题型：
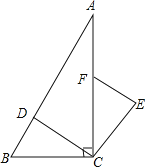
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D，F分别在AB，AC上，CF＝CB．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD．求∠BDC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下四个结论：①abc=0；②a+b+c＞0；③a＞b；④b2﹣4ac＜0；其中正确的结论有（ ） 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
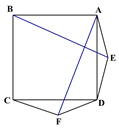
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF，连接AF，BE．
（图1） （图2） （备用图）
（1）请判断：AF与BE的数量关系是_____________，位置关系______________；
（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予证明；
（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
