
【题目】先阅读,后解答: ![]() =
= ![]() =
= ![]() =3+
=3+ ![]()
像上述解题过程中, ![]() ﹣
﹣ ![]() 与
与 ![]() +
+ ![]() 相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
相乘,积不含有二次根式,我们可将这两个式子称为互为有理化因式,上述解题过程也称为分母有理化,
(1)![]() 的有理化因式是;
的有理化因式是; ![]() +2的有理化因式是
+2的有理化因式是
(2)将下列式子进行分母有理化: ![]() =;
=; ![]() = .
= .
(3)已知a= ![]() ,b=2﹣
,b=2﹣ ![]() ,比较a与b的大小关系.
,比较a与b的大小关系.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形ABCD对折,得折痕PQ,展开后再沿MN翻折,使点C恰好落在折痕PQ上的点C′处,点D落在D′处,其中M是BC的中点且MN与折痕PQ交于F.连接AC′,BC′,则图中共有等腰三角形的个数是( )
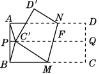
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线C1:y=x2+bx+c经过原点,与x轴的另一个交点为(2,0),将抛物线C1向右平移m(m>0)个单位得到抛物线C2 , C2交x轴于A,B两点(点A在点B的左边),交y轴于点C.
(1)求抛物线C1的解析式及顶点坐标;
(2)以AC为斜边向上作等腰直角三角形ACD,当点D落在抛物线C2的对称轴上时,求抛物线C2的解析式;
(3)若抛物线C2的对称轴存在点P,使△PAC为等边三角形,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR,②QP∥AR,③△BPR≌△QPS中一定正确的是( )

A. 全部正确 B. 仅①和②正确 C. 仅①正确 D. 仅①和③正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是( ) 
A.h≤17cm
B.h≥8cm
C.15cm≤h≤16cm
D.7cm≤h≤16cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区居民利用“健步行APP”开展健步走活动,为了解居民的健步走情况,小文同学调查了部分居民某天行走的步数![]() 单位:千步
单位:千步![]() ,并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
,并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图.
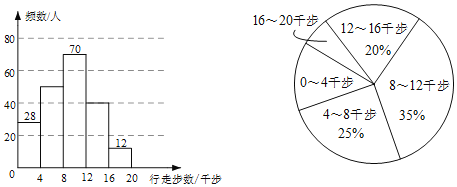
有下面四个推断:
![]() 小文此次一共调查了200位小区居民;
小文此次一共调查了200位小区居民;
![]() 行走步数为
行走步数为![]() 千步的人数超过调查总人数的一半;
千步的人数超过调查总人数的一半;
![]() 行走步数为
行走步数为![]() 千步的人数为50人;
千步的人数为50人;
![]() 行走步数为
行走步数为![]() 千步的扇形圆心角是
千步的扇形圆心角是![]() .
.
根据统计图提供的信息,上述推断合理的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com