
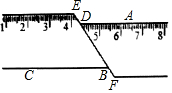
 如图:一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠DBC=50°,则∠ADE的度数为130°.
如图:一把直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠DBC=50°,则∠ADE的度数为130°.  期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:填空题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对我省七年级学生视力情况的调查 | |
| B. | 对一批LED节能灯使用寿命的调查 | |
| C. | 对量子通信卫星上零部件质量的调查 | |
| D. | 对“最强大脑”节目收视率的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com