
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
【答案】(1)证明见解析;(2)m1=1,m2=-3.
【解析】
试题(1)根据关于x的一元二次方程x2+(m+3)x+m+1=0的根的判别式△=b2﹣4ac的符号来判定该方程的根的情况;
(2)根据根与系数的关系求得x1+x2=﹣(m+3),x1x2=m+1;然后由已知条件“|x1﹣x2|=2![]() ”可以求得(x1﹣x2)2=(x1+x2)2﹣4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程.
”可以求得(x1﹣x2)2=(x1+x2)2﹣4x1x2=8,从而列出关于m的方程,通过解该方程即可求得m的值;最后将m值代入原方程并解方程.
试题解析: (1)∵△=(m+3)2﹣4(m+1)=(m+1)2+4,
∵无论m取何值,(m+1)2+4恒大于0,
∴原方程总有两个不相等的实数根.
(2)∵x1,x2是原方程的两根,
∴x1+x2=﹣(m+3),x1x2=m+1,
∵|x1﹣x2|=2![]()
∴(x1﹣x2)2=(2![]() )2,
)2,
∴(x1+x2)2﹣4x1x2=8,
∴[﹣(m+3)]2﹣4(m+1)=8∴m2+2m﹣3=0,
解得:m1=﹣3,m2=1.
当m=﹣3时,原方程化为:x2﹣2=0,
解得:x1=![]() ,x2=﹣
,x2=﹣![]() ,
,
当m=1时,原方程化为:x2+4x+2=0,
解得:x1=﹣2+![]() ,x2=﹣2﹣
,x2=﹣2﹣![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
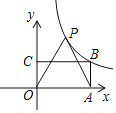
【题目】如图,矩形OABC的顶点A,C分别在x轴,y轴上,顶点B在第一象限,AB=1.将线段OA绕点O按逆时针方向旋转60°得到线段OP,连接AP,反比例函数![]() (k≠0)的图象经过P,B两点,则k的值为______________.
(k≠0)的图象经过P,B两点,则k的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
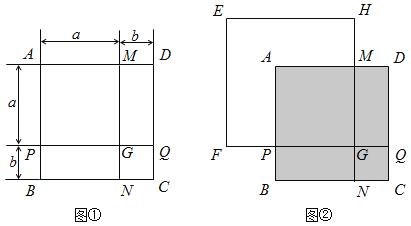
(1)利用正方形ABCD面积的不同表示方法,直接写出![]() 、
、![]() 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;
(2)若m满足![]() ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求![]() 的值;
的值;
(3)若将正方形EFGH的边![]() 、
、![]() 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A是函数y=﹣![]() (x<0)图象上的一点,连结AO并延长交函数y=﹣
(x<0)图象上的一点,连结AO并延长交函数y=﹣![]() (x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____.
(x>0)的图象于点B,点C是x轴上一点,且AC=AO,则△ABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连接AD,AC,BC,BD,若AD=AC=AB,则下列结论:①AE垂直平分CD,②AC平分∠BAD,③△ABD是等边三角形,④∠BCD的度数为150°,其中正确的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=3cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发。
(1)几秒钟后,P、Q间的距离等于4![]() cm?
cm?
(2)几秒种后,△BPQ的面积与四边形CQPA的面积相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB∶BC=3∶2,∠DAB=60°,E在AB上,且AE∶EB=1∶2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP∶DQ等于
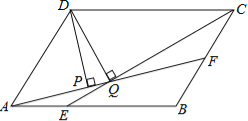
A.3∶4 B.![]() ∶
∶![]() C.
C.![]() ∶
∶![]() D.
D.![]() ∶
∶![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com