
【题目】如图①,正方形ABCD是由两个长为a、宽为b的长方形和两个边长分别为a、b的正方形拼成的.
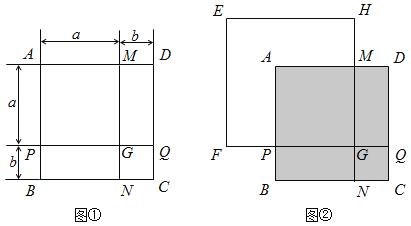
(1)利用正方形ABCD面积的不同表示方法,直接写出![]() 、
、![]() 、ab之间的关系式,这个关系式是 ;
、ab之间的关系式,这个关系式是 ;
(2)若m满足![]() ,请利用(1)中的数量关系,求
,请利用(1)中的数量关系,求![]() 的值;
的值;
(3)若将正方形EFGH的边![]() 、
、![]() 分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
分别与图①中的PG、MG重叠,如图②所示,已知PF=8,NH=32,求图中阴影部分的面积(结果必须是一个具体数值).
【答案】(1)![]() ;(2)-2019;(3)576
;(2)-2019;(3)576
【解析】
(1)由正方形ABCD的面积等于边长的平方,或者等于两个小正方形的面积+两个小长方形的面积,可得关系式;
(2)设2020﹣m=a,m﹣2019=b,由完全平方公式可求解;
(3)设正方形EFGH的边长为x,则PG=x﹣8,NG=32﹣x,由S阴=S正方形APGM+2S长方形PBNG+S正方形CQGN,代入后利用完全平方公式即可求解.
(1)根据正方形ABCD的面积等于边长的平方,即(a+b)2,也等于两个小正方形的面积+两个小长方形的面积,即a2+b2+2ab,∴(a+b)2=a2+b2+2ab.
故答案为:(a+b)2=a2+b2+2ab;
(2)设2020﹣m=a,m﹣2019=b,
则(2020﹣m)(m﹣2019)=ab,a+b=1,a2+b2=4039.
∵(a+b)2=a2+b2+2ab,∴12=4039+2ab,∴ab=﹣2019,∴(2020﹣m)(m﹣2019)=﹣2019;
(3)设正方形EFGH的边长为x,则PG=x﹣8,NG=32﹣x.
∵S阴=S正方形APGM+2S长方形PBNG+S正方形CQGN,∴![]() ,
,
∵(a+b)2=a2+b2+2ab,∴![]() 242=576.
242=576.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,∠BAC=∠DAE=90°,AD=AE,AB=AC,且B、D、E三点在一条直线上.
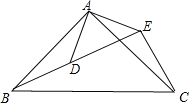
(1)求证:BD=CE.
(2)求∠BEC的度数.
(3)写出BE与AE、CE的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A. ![]() B.
B. ![]() C. 5 D.
C. 5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系.
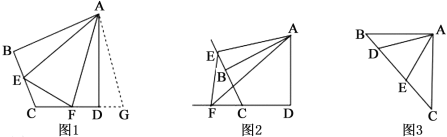
(1)思路梳理
将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF之间的数量关系为__;
(2)类比引申
如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=![]() ∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x﹣2与两坐标轴分别交于点A,C,交y=![]() (x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(x>0)于点P,PQ⊥x轴于点Q,CQ=1.
(1)求反比例函数解析式;
(2)平行于y轴的直线x=m分别交y=x﹣2,y=![]() (x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
(x>0)于点D,B(B在线段AP上方),若S△BOD=2,求m值.
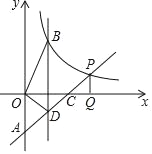
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(m+3)x+m+1=0.
(1)求证:无论m取何值,原方程总有两个不相等的实数根;
(2)若x1,x2是原方程的两根,且|x1-x2|=2![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发市场,草莓的批发价格是每箱![]() 元,苹果的批发价格是每箱
元,苹果的批发价格是每箱![]() 元.
元.
(1)若李心批发草莓,苹果共![]() 箱,刚好花费
箱,刚好花费![]() 元,则他购买草莓、苹果各多少箱.
元,则他购买草莓、苹果各多少箱.
(2)李心有甲,乙两个店铺,每个店铺在同一时间段内都能售出草莓,苹果两种水果合计![]() 箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为
箱,并且每售出一箱草莓和苹果,甲店铺获毛利润分别为![]() 元和
元和![]() 元,乙店铺获毛利润分别为
元,乙店铺获毛利润分别为![]() 元和
元和![]() 元.现在,李心要将批发购进的
元.现在,李心要将批发购进的![]() 箱草莓,
箱草莓,![]() 箱苹果分配给每个店铺各
箱苹果分配给每个店铺各![]() 箱.设分配给甲店草莓
箱.设分配给甲店草莓![]() 箱.
箱.
①根据信息填表:
草莓数量(箱) | 苹果数量(箱) | 合计(箱) | |
甲店 |
|
| |
乙店 |
|
②设李心获取的总毛利润为![]() 元,
元,
(1)求![]() 与
与![]() 的函数关系式:
的函数关系式:
(2)若在保证乙店铺获得毛利润不少于![]() 元的前提下,应怎样分配水果,使总毛利润
元的前提下,应怎样分配水果,使总毛利润![]() 最大,最大的总毛利润是多少元.
最大,最大的总毛利润是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的两个实数根.
(1)是否存在实数a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,请你说明理由;
(2)求使(x1+1)(x2+1)为正整数的实数a的整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com