
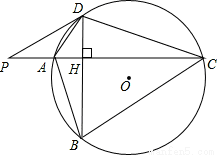
如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若tan∠ADB=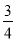 ,PA=
,PA=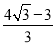 AH,求BD的长;
AH,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积.
(1)PD与圆O相切;理由见解析;(2)25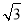 ;(3)900+
;(3)900+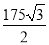 .
.
【解析】
试题分析:(1)首先连接DO并延长交圆于点E,连接AE,由DE是直径,可得∠DAE的度数,又由∠PDA=∠ABD=∠E,可证得PD⊥DO,即可得PD与圆O相切于点D;
(2)首先由tan∠ADB=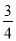 ,可设AH=3k,则DH=4k,又由PA=
,可设AH=3k,则DH=4k,又由PA=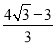 AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE•cos30°=25
AH,易求得∠P=30°,∠PDH=60°,连接BE,则∠DBE=90°,DE=2r=50,可得BD=DE•cos30°=25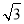 ;
;
(3)由(2)易得HC=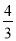 (25
(25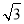 -4k),又由PD2=PA×PC,可得方程:(8k)2=(4
-4k),又由PD2=PA×PC,可得方程:(8k)2=(4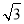 -3)k×[4
-3)k×[4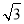 k+
k+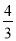 (25
(25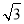 -4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.
-4k)],解此方程即可求得AC的长,继而求得四边形ABCD的面积.
试题解析:(1)PD与圆O相切.
理由:如图,连接DO并延长交圆于点E,连接AE,
∵DE是直径,
∴∠DAE=90°,
∴∠AED+∠ADE=90°,
∵∠PDA=∠ABD=∠AED,
∴∠PDA+∠ADE=90°,
即PD⊥DO,
∴PD与圆O相切于点D;
(2)∵tan∠ADB=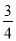
∴可设AH=3k,则DH=4k,
∵PA=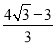 AH,
AH,
∴PA=(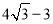 )k,
)k,
∴PH=4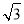 k,
k,
∴在Rt△PDH中,tan∠P=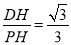 ,
,
∴∠P=30°,∠PDH=60°,
∵PD⊥DO,
∴∠BDE=90°-∠PDH=30°,
连接BE,则∠DBE=90°,DE=2r=50,
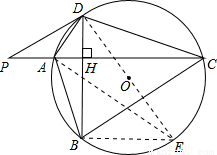
∴BD=DE•cos30°=25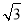 ;
;
(3)由(2)知,BH=25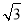 -4k,
-4k,
∴HC=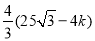 ,
,
又∵PD2=PA×PC,
∴(8k)2=(4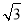 -3)k×[4
-3)k×[4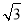 k+
k+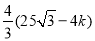 ],
],
解得:k=4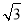 -3,
-3,
∴AC=3k+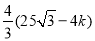 =24
=24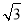 +7,
+7,
∴S四边形ABCD=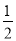 BD•AC=
BD•AC=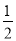 ×25
×25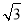 ×(24
×(24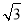 +7)=900+
+7)=900+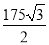 .
.
考点:圆的综合题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:解答题
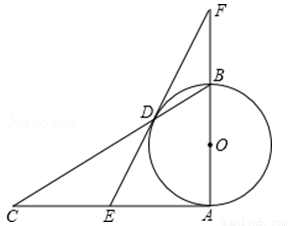
已知:如图,在Rt△ABC中,∠A=90°,以AB为直径作⊙O,BC交⊙O于点D,E是边AC的中点,ED、AB的延长线相交于点F.
求证:(1)DE为⊙O的切线.
(2)AB•DF=AC•BF.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:选择题
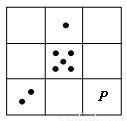
现有3×3的方格,每个小方格内均有数目不同的点图,要求方格内每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图中给出了部分点图,则P处所对应的点图是( )

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考一模数学试卷(解析版) 题型:选择题
环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省苏州市高新区中考学二模数试卷(解析版) 题型:填空题
某剧团甲乙两个女舞蹈队的平均身高都是1.65米,甲队身高的方差是S甲2=1.5,乙队身高的方差是S乙2=2.4,那么两队中身高更整齐的是 队.(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省盐城市亭湖区中考一模数学试卷(解析版) 题型:解答题
某经销商代理销售一种手机,按协议,每卖出一部手机需另交品牌代理费100元,已知该种手机每部进价800元,销售单价为1200元时,每月能卖出100部,市场调查发现,若每部手机每让利50元,则每月可多售出40部.
(1)若每月要获取36000元利润,求让利价
(利润=销售收入-进货成本-品牌代理费)
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com