练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2（2x+1）-（10x+1）=6．
    考点：解一元一次方程
    专题：计算题
    分析：方程去括号，移项合并，将x系数化为1，即可求出解．
    解答：解：去括号得：4x+2-10x-1=6，
    移项合并得：-6x=5，
    解得：x=-
    5
    6
    ．
    点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    若2a-3b=0，且b≠0，则
    4a2-2ab-b2
    ab-2a2
    =（　　）
    A、-
    4
    3
    B、-
    10
    3
    C、-
    5
    3
    D、-
    2
    3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （-
    5
    6
    ）÷（-3
    1
    6
    ）÷[
    1
    24
    ×（-1
    1
    4
    ）]-0.25÷
    1
    4
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直线y=k1x+b与双曲线y=
    k2
    x
    相交于A（1，2）、B（m，-1）两点．
    （1）求直线和双曲线的解析式；
    （2）求△OAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解无理方程：2-x2=
    		5-4x
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知∠COB=4∠AOC，OD平分∠AOB，且∠COD=36°，求∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

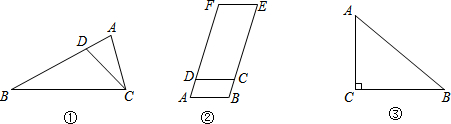
    如果两个多边形不仅相似（相似比不等于1），而且有一条公共边，那么就称这两个多边形是共边相似多边形．例如，图①中，△ABC与△ACD是共AC边相似三角形，图②中，?ABCD与?CEFD是共CD边相似四边形．

    （1）判断下列命题的真假（在相应括号内填上“真”或“假”）：
    ①正三角形的共边相似三角形是正三角形．
     

    ②如果两个三角形是位似三角形，那么这两个三角形不可能是共边相似三角形．
     

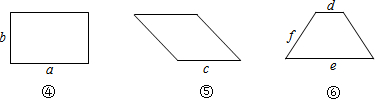
    （2）如图③，在△ABC中，∠C=90°，∠A=50°，画2个不全等的三角形，使这2个三角形均是与△ABC共BC边的相似三角形．（要求：画图工具不限，不写画法，保留画图痕迹或有必要的说明）
    （3）图④是相邻两边长分别为a、b（a＞b）的矩形，图⑤是边长为c的菱形，图⑥是两底长分别为d、e，腰长为f（0＜e-d＜2f）的等腰梯形，判断这三个图形是否存在共边相似四边形？如果存在，直接写出它们的共边相似四边形各边的长度．
    （4）根据（1）、（2）和（3）中获得的经验回答：如果一个多边形存在它的共边相似多边形，那么它必须满足条件：
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，∠AOB=38°，∠BOC=96°，OD是∠AOC的平分线，求∠BOD的度数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）如图1，已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE，∠BAD=∠CAE=90°，连接BE和CD相交于点O，AB交CD于点F，AC交BE于点G，求证：BE=DC，且BE⊥DC．

    请补充完整证明“BE=DC，且BE⊥DC”的推理过程；
    证明：∵△ABD和△ACE都是等腰直角三角形（已知）
    ∴AB=AD，AE=AC（等腰直角三角形定义）
    又∵∠BAD=∠CAE=90°（已知）
    ∴∠BAD+∠BAC=
     
    （等式性质）
    即：
     

    ∴△ABE≌△ADC（
     
    ）
    ∴BE=DC（全等三角形的对应边相等）
    ∠ABE=∠ADC（全等三角形的对应角相等）
    又∵∠BFO=∠DFA（
     
    ）
    ∠ADF+∠DFA=90°（直角三角形的两个锐角互余）
    ∴∠ABE+∠BFO=90°（等量代换）
    ∴
     
     即BE⊥DC
    （2）探究：若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE，连接BE和CD相交于点O，AB交CD于点F，AC交BE于G，如图2，则BE与DC还相等吗？若相等，请证明，若不相等，说明理由；并请求出∠BOD的度数？

    查看答案和解析>>

    同步练习册答案