
【题目】如图,已知OABC的顶点A,C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为( )
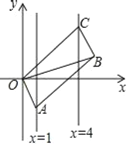
A.3B.4C.5D.6
【答案】C
【解析】
过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E.则OB=![]() .由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
.由于四边形OABC是平行四边形,所以OA=BC,又由平行四边形的性质可推得∠OAF=∠BCD,则可证明△OAF≌△BCD,所以OE的长固定不变,当BE最小时,OB取得最小值,从而可求.
解:过点B作BD⊥直线x=4,交直线x=4于点D,过点B作BE⊥x轴,交x轴于点E,直线x=1与OC交于点M,与x轴交于点F,直线x=4与AB交于点N,如图:
∵四边形OABC是平行四边形,
∴∠OAB=∠BCO,OC∥AB,OA=BC,
∵直线x=1与直线x=4均垂直于x轴,
∴AM∥CN,
∴四边形ANCM是平行四边形,
∴∠MAN=∠NCM,
∴∠OAF=∠BCD,
∵∠OFA=∠BDC=90°,
∴∠FOA=∠DBC,
在△OAF和△BCD中,
 ,
,
∴△OAF≌△BCD.
∴BD=OF=1,
∴OE=4+1=5,
∴OB=![]() .
.
由于OE的长不变,所以当BE最小时(即B点在x轴上),OB取得最小值,最小值为OB=OE=5.
故选:C.



科目:初中数学 来源: 题型:
【题目】已知直线y=kx(k≠0)经过点(12,﹣5),将直线向上平移m(m>0)个单位,若平移后得到的直线与半径为6的⊙O相交(点O为坐标原点),则m的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市居民用水情况,在某小区随机抽查了20户家庭,并将这些家庭的月用水量进行统计,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 8 | 13 |
户数 | 4 | 5 | 7 | 3 | 1 |
则关于这20户家庭的月用水量,下列说法正确的是( )
A.中位数是5B.平均数是5C.众数是6D.方差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持大学生勤工俭学,市政府向某大学生提供了![]() 万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件
万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件![]() 元.每天还要支付其他费用
元.每天还要支付其他费用![]() 元.该产品每天的销售量
元.该产品每天的销售量![]() 件
件![]() 与销售单价
与销售单价![]() 元
元![]() 关系为
关系为![]() .
.
(1)设每天的利润为![]() 元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元?
元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元?![]() 注:每天的利润
注:每天的利润![]() 每天的销售利润一每天的支出费用
每天的销售利润一每天的支出费用![]()
(2)若销售单价不得低于其生产成本,且销售每件产品的利润率不能超过![]() ,则该学生最快用多少天可以还清无息贷款?
,则该学生最快用多少天可以还清无息贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
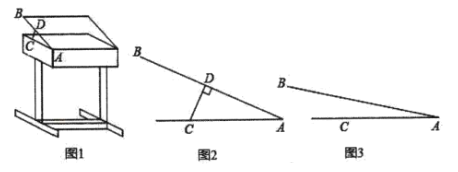
【题目】某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1,![]() 可绕点
可绕点![]() 旋转,在点
旋转,在点![]() 处安装一根长度一定且
处安装一根长度一定且![]() 处固定,可旋转的支撑臂
处固定,可旋转的支撑臂![]() ,
,![]() .
.
(1)如图2,当![]() 时,
时,![]() ,求支撑臂
,求支撑臂![]() 的长;
的长;
(2)如图3,当![]() 时,求
时,求![]() 的长.(结果保留根号)
的长.(结果保留根号)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,BC=8,点E是BC边上的一个动点(不与点B.C重合),连结AE,并作EF⊥AE,交CD边于点F,连结AF.设BE=x,CF=y.
(1)求证:△ABE∽△ECF;
(2)当x为何值时,y的值为2;

查看答案和解析>>
科目:初中数学 来源: 题型:
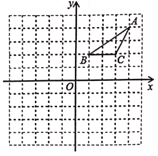
【题目】在正方形网格中建立如图所示的平面直角坐标系![]() ,
,![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标是
的坐标是![]() ,请解答下列问题:
,请解答下列问题:
(1)将![]() 向左平移5个单位长度,画出平移后的
向左平移5个单位长度,画出平移后的![]() ,并写出点
,并写出点![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(2)点![]() 为位似中心,在网格中画出
为位似中心,在网格中画出![]() ,使
,使![]() 与
与![]() 相似,且
相似,且![]() 与
与![]() 的位似比为1:1
的位似比为1:1
(3)![]() (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (k>0).
(k>0).
(1)当k=![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程![]() 有两个不相等的实数根;
有两个不相等的实数根;
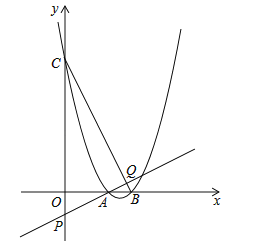
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com