Question

【题目】课题学习：我们知道二次函数的图象是抛物线，它也可以这样定义：如果一个动点M（x，y）到定点A（0，m）（m＞0）的距离与它到定直线y=﹣m的距离相等，那么动点M形成的图形就是抛物线y=ax2（a＞0）的图象，如图所示．

（1）探究：当x≠0时，a与m有何数量关系？
（2）应用：已知动点M（x，y）到定点A（0，4）的距离与到定直线y=﹣4的距离相等，请写出动点M形成的抛物线的解析式．
（3）拓展：根据抛物线的平移变换，抛物线y= （x﹣1）2+2的图象可以看作到定点A（ ， ）的距离与它到定直线y=的距离相等的动点M（x，y）所形成的图形．
（4）若点D的坐标是（1，8），在（2）中求得的抛物线上是否存在点P，使得PA+PD最短？若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

【答案】
（1）

解：由定义可知，MA=MB，

∴x2+（y﹣m）2=（y+m）2，

∵y=ax2，

∴x2= ，

∴ =4my，

∴a=

（2）

解：由（1）可知，a= ，

∴抛物线的解析式为y= x2．

（3）1；3；1
（4）

解：如图所示，过点D作直线y=﹣4的垂线垂足为M，与抛物线的交点就是的点P，此时PA+PD=PD+PM最短（垂线段最短），

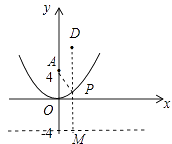
此时点P坐标（1， ）．

【解析】解：（3）∵抛物线顶点坐标（1，2），a=1，
∴抛物线y= （x﹣1）2+2的图象可以看作到定点A（1，3）的距离与它到定直线y=1的距离相等的动点M（x，y）所形成的图形．
所以答案是1，3，1．
【考点精析】关于本题考查的二次函数的图象，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能得出正确答案．