
【题目】
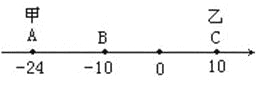
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是____________.
【答案】(1)3.4秒 (2)2或者5秒(3)-44
【解析】试题分析:(1)可设x秒后甲与乙相遇,根据甲与乙的路程差为34,可列出方程求解即可;
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解;
(3)分①原点O是甲蚂蚁P与乙蚂蚁Q两点的中点;②乙蚂蚁Q是甲蚂蚁P与原点O两点的中点;③甲蚂蚁P是乙蚂蚁Q与原点O两点的中点,三种情况讨论即可求解.
试题解析:(1)设x秒后甲与乙相遇,则
4x+6x=34,
解得x=3.4,
甲乙在3.4秒后相遇.
(2)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
(3)①甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:-24+4×2-4y;乙表示的数为:10-6×2-6y,
依据题意得:-24+4×2-4y=10-6×2-6y,
解得:y=7,
相遇点表示的数为:-24+4×2-4y=-44(或:10-6×2-6y=-44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:-24+4×5-4y;乙表示的数为:10-6×5-6y,
依据题意得:-24+4×5-4y=10-6×5-6y,
解得:y=-8(不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】某商店进行促销活动,如果将进价为8元/件的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品的单价每涨1元,其销售量就要减少10件,问将售价定为多少元/件时,才能使每天所赚的利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:b是最小的正整数,且a、b满足![]() =0,请回答问题
=0,请回答问题
(1)请直接写出a、b、c的值。
a=__________; b=__________;c=__________
(2)a、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到2之间运动时(即0≤x≤2时),请化简式子:![]() (请写出化简过程)
(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB。请问:BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一次函数y=kx+b的图象.
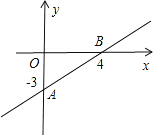
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干个偶数按每行8个数排成如图所示的阵列:

(1)图中方框内的9个数的和与中间的数有什么关系?
(2)小亮画了一个方框,他所画的方框内9个数的和为360,求这9个数;(直接写出答案)。
(3)小霞也画了一个方框,方框内9个数的和为262,你能写出这9个数吗?如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量![]() 个)与它的定价
个)与它的定价![]() (元/个)的关系如图所示:
(元/个)的关系如图所示:
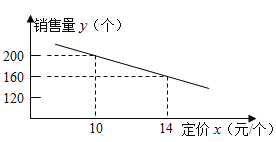
(1)求这种文具盒每个星期的销售量![]() 个)与它的定价
个)与它的定价![]() (元/个)之间的函数关系式(不必写出自变量
(元/个)之间的函数关系式(不必写出自变量![]() 的取值范围)
的取值范围)
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年3月5日,实验中学组织全体学生参加了“走出校门,服务社会”的活动。九年级一班小明同学统计了该天本班学生打扫街道,去敬老院服务和到社区文艺演出的人数,并做了如下直方图和扇形统计图。请根据小明同学所作的两个图形,解答:
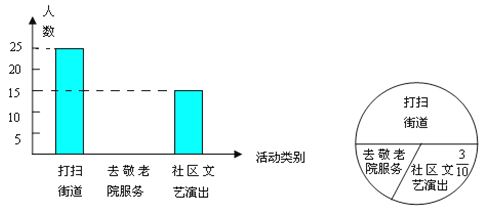
(1)九年级一班有多少名学生?
(2)补全直方图的空缺部分。
(3)若九年级有800名学生,估计该年级去敬老院的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com