
【题目】如图,是一次函数y=kx+b的图象.
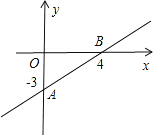
(1)求这个一次函数的解析式?
(2)试判断点P(1,-1)是否在这个一次函数的图象上?
(3)求原点O到直线AB的距离.
【答案】(1)一次函数的解析式y=![]() x-3;(2)不成立,(3)
x-3;(2)不成立,(3)![]() .
.
【解析】试题分析:(1)根据待定系数法即可求解;
(2)把P的坐标代入解析式进行检验即可;
(3)在直角△OAB中,根据勾股定理可以求得AB的长,再根据面积公式即可求解.
试题解析:(1)设函数的解析式为y=kx+b(k≠0),
∵图象与x,y轴交点的坐标分别为(4,0),(0,-3),
∴把两点代入函数解析式得![]() ,解得
,解得 ,
,
故一次函数的解析式y=![]() x-3;
x-3;
(2)把P(1,-1)代入解析式得-1=![]() -3,不成立,
-3,不成立,
故此点不在这个一次函数的图象上;
(3)在△OAB中|OB|=4,|OA|=|-3|=3,由勾股定理得AB2=OA2+OB2,即AB2=32+42,
则AB=5,
设原点O到直线AB的距离为h.则![]() h×|AB|=
h×|AB|=![]() |OA||OB|,
|OA||OB|,
即h=![]() =
=![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某空调器销售商,今年四月份销出空调a台,五月份销售空调比四月份的2倍少1台,六月份销售空调比前两个月的总和的4倍还多5台.
(1)用含a代数式分别表示该销售商今年四月份、五月份、六月份销售空调多少台?.
(2)若a=220,求六月份销售的空调总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,学习委员小兵每周对各小组合作学习的情况进行了综合评分.下表是其中一周的统计数据:
组 别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
分 值 | 90 | 95 | 90 | 88 | 90 | 92 | 85 |
这组数据的中位数和众数分别是
A. 88,90 B. 90,90 C. 88,95 D. 90,95
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=(x-1)2+2,下列说法正确的是( )
A. 图像与y轴的交点坐标为(0,2) B. 图像的对称轴在y轴的左侧
C. y的最大值为2 D. 当x>1时,y的值随x值的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
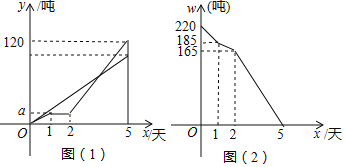
【题目】某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.设甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间s(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米 吨,a= .
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
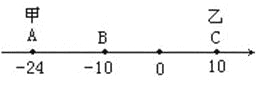
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A、B、C三点的距离和为40个单位?
(3)当甲到A、B、C三点的距离和为40个单位时,甲调头返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E。
(1)∠B= 度.
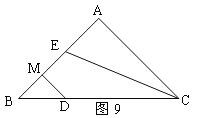
(2)如图9,若点D在斜边BC上,DM垂直平分BE,垂足为M。求证:BD=AE;
(3)如图10,过点B作BF⊥CE,交CE的延长线与点F。若CE=6,求△BEC的面积。
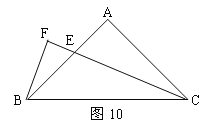
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),
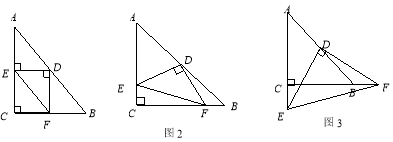
(1)易证![]() +
+![]() =
=![]()
![]() .
.
![]() (2)当∠EDF绕
(2)当∠EDF绕![]() 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,![]() 、
、![]() 、
、![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数![]() 的图象为直线
的图象为直线![]() ,一次函数
,一次函数![]() 的图象为直线
的图象为直线![]() ,若
,若![]() ,且
,且![]() ,我们就称直线
,我们就称直线![]() 与直线
与直线![]() 互相平行.已知一次函数
互相平行.已知一次函数![]() 的图象为直线
的图象为直线![]() ,过点
,过点![]() 且与已知直线
且与已知直线![]() 平行的直线为
平行的直线为![]() 。
。
解答下面的问题:
(1)求![]() 的函数表达式;
的函数表达式;
(2)设直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求
轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求![]() 和
和![]() 两平行线之间的距离 ;
两平行线之间的距离 ;
(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标。
(4)在![]() 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com