
【题目】如图,A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作CD∥OF交AB的延长线于点D,延长AF交直线CD于点H.
(1)求证:CD是半圆O的切线;
(2)若DH=![]() ,求EF的长和半径OA的长.
,求EF的长和半径OA的长.
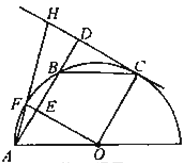
【答案】(1)证明过程见解析;(2)EF=2-![]() ;OA=2.
;OA=2.
【解析】试题分析:(1)连接OB,根据已知条件得到△AOB是等边三角形,得到∠AOB=60°,根据圆周角定理得到∠AOF=∠BOF=30°,根据平行线的性质得到OC⊥CD,由切线的判定定理即可得到结论;(2)根据平行线的性质得到∠DBC=∠EAO=60°,解直角三角形得到BD=![]() BC=
BC=![]() AB,推出AE=
AB,推出AE=![]() AD,根据相似三角形的性质得到
AD,根据相似三角形的性质得到![]() ,求得EF=2﹣
,求得EF=2﹣![]() ,根据直角三角形的性质即可得到结论.
,根据直角三角形的性质即可得到结论.
试题解析:(1)连接OB, ∵OA=OB=OC, ∵四边形OABC是平行四边形, ∴AB=OC,
∴△AOB是等边三角形, ∴∠AOB=60°, ∵∠FAD=15°, ∴∠BOF=30°, ∴∠AOF=∠BOF=30°,
∴OF⊥AB, ∵CD∥OF, ∴CD⊥AD, ∵AD∥OC, ∴OC⊥CD, ∴CD是半圆O的切线;
(2)∵BC∥OA, ∴∠DBC=∠EAO=60°, ∴BD=![]() BC=
BC=![]() AB, ∴AE=
AB, ∴AE=![]() AD, ∵EF∥DH,∴△AEF∽△ADH,
AD, ∵EF∥DH,∴△AEF∽△ADH,
∴![]() , ∵DH=6﹣3
, ∵DH=6﹣3![]() , ∴EF=2﹣
, ∴EF=2﹣![]() , ∵OF=OA, ∴OE=OA﹣(2﹣
, ∵OF=OA, ∴OE=OA﹣(2﹣![]() ),
),
∵∠AOE=30°, ∴![]() =
=![]() =
=![]() , 解得:OA=2.
, 解得:OA=2.


科目:初中数学 来源: 题型:
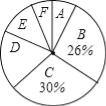
【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截止2018年5月末,中国人民银行公布的数据显示,我国外汇的储备规模约为3.11×104亿元美元,则3.11×104亿表示的原数为( )
A. 2311000亿 B. 31100亿 C. 3110亿 D. 311亿
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据考证,单个雪花的质量在0.000 25克左右,这个数用科学记数法表示为( )
A.2.5×10-3
B.2.5×10-4
C.2.5×10-5
D.-2.5×10-4
查看答案和解析>>
科目:初中数学 来源: 题型:
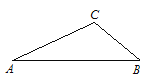
【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣1)2﹣3(a≠0)的图象与y轴交于点A(0,﹣2),顶点为B.
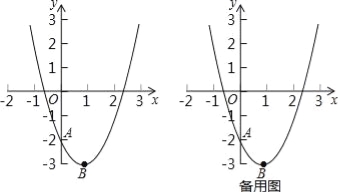
(1)试确定a的值,并写出B点的坐标;
(2)若一次函数的图象经过A、B两点,试写出一次函数的解析式;
(3)试在x轴上求一点P,使得△PAB的周长取最小值;
(4)若将抛物线平移m(m≠0)个单位,所得新抛物线的顶点记作C,与原抛物线的交点记作D,问:点O、C、D能否在同一条直线上?若能,请求出m的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com