
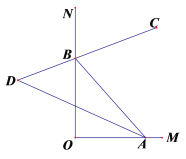
【题目】如图,∠MON=90°点A、B分别在线段OM、ON上(不与点O重合),BC是∠ABN的平分线,BC的反向延长线与∠BAO的平分线交于点D.
(1)若∠BAO=60°,求∠ABC和∠D的度数.
(2)若∠BAO=![]() °,求∠ABC和∠D的度数.
°,求∠ABC和∠D的度数.
(3)若△ABD中有一个角是另一个角的3倍,直接写出此时∠ABC的度数.
【答案】⑴∠ABC=75°;∠D=45°;⑵∠ABC=45+![]() x;∠D=45°;⑶60°或78.75°.
x;∠D=45°;⑶60°或78.75°.
【解析】
(1)先求出∠ABN=150°,再根据角平分线得出∠ABC的度数,∠BAD的度数,最后由外角性质可得∠D度数即可;
(2)设∠BAD=![]() °,利用外角性质和角平分线定义求得∠ABC=45°+
°,利用外角性质和角平分线定义求得∠ABC=45°+![]()
![]() °,利用∠D=∠ABC-∠BAD即可得答案;
°,利用∠D=∠ABC-∠BAD即可得答案;
(3)分∠D=3∠DAB,∠DBA=3∠DAB,∠DBA=3∠D三种情况进行讨论即可.
(1)∵∠BAO=60°、∠MON=90°,
∴∠ABN=∠BAO+∠MON=150°,
∵BC平分∠ABN、AD平分∠BAO,
∴∠ABC=![]() ∠ABN=75°,∠BAD=
∠ABN=75°,∠BAD=![]() ∠BAO=30°,
∠BAO=30°,
∴∠D=∠CBA-∠BAD=45°;
(2)∵∠BAO=x°、∠MON=90°,
∴∠ABN=∠BAO+∠MON=(90+x)°,
∵BC平分∠ABN、AD平分∠BAO,
∴∠ABC=![]() ∠ABN=(45+
∠ABN=(45+![]() x)°,∠BAD=
x)°,∠BAD=![]() ∠BAO=
∠BAO=![]() x°,
x°,
∴∠D=∠CBA-∠BAD=45°;
(3)由(2)可知∠D的度数不变,∠D=45°,
若∠D=3∠DAB,则∠DAB=15°,
∵AD平分∠BAO,∴∠BAO=2∠DAB=30°,
∴∠ABN=∠BAO+∠MON=120°,
∵BC平分∠ABN,
∴∠ABC=![]() ∠ABN=60°;
∠ABN=60°;
若∠DBA=3∠DAB,
∵∠DBA+∠DAB=135°,
∴∠DAB=33.75°,
∵AD平分∠BAO,∴∠BAO=2∠DAB=67.5°,
∴∠ABN=∠BAO+∠MON=157.5°,
∵BC平分∠ABN,
∴∠ABC=![]() ∠ABN=78.75°;
∠ABN=78.75°;
若∠DBA=3∠D,此种情况不存在,
综上,∠ABC=60°或78.75°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】假期,某校为了勤工俭学,要完成整个A小区的绿化工作,开始由七年级单独工作了4天,完成整个绿化工作的三分之一,这时九年级也参加工作,两个年级又共同工作了2天,才全部完成整个绿化工作,则由九年级单独完成整个绿化工作需要____天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强作出边长为1的第1个等边△A1B1C1 , 计算器面积为S1 , 然后分别取△A1B1C1三边的中点A2、B2、C1 , 作出第2个等边△A2B2C2 , 计算其面积为S2 , 用同样的方法,作出第3个等边△A3B3C3 , 计算其面积为S3 , 按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20= . 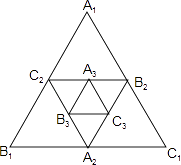
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点D的对应点D′.
(1)根据特征画出平移后的△A′B′C′;
(2)利用网格的特征,画出AC边上的高BE并标出画法过程中的特征点;
(3)△A′B′C′的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与x轴相交于点A,与y轴相交于点B.
(1)求A,B两点的坐标;
(2)过B点作直线与x轴交于点P,若△ABP的面积为![]() ,试求点P的坐标.
,试求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
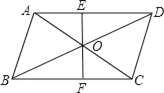
【题目】如图平行四边形ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC分别交于点E,F,已知AE=3,BF=5
(1)求BC的长;
(2)如果两条对角线长的和是20,求三角形△AOD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以2cm/s的速度沿如图所示的边框从B-C-D-E-F-A的路径运动,记△ABP的面积为S (cm2), S与运动时间t (s)的关系如图所示,若AB=6cm,请回答下列问题:
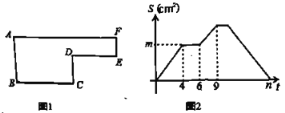
(1)如图中BC=______cm, CD=______cm,DE=______cm
(2)求出如图中边框所围成图形的面积;
(3)求如图中m、n的值;
(4)分别求出当点P在线段BC和DE上运动时S与t的关系式,并写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com