
【题目】若菱形两条对角线之比为3:4,周长是40cm,则它的面积是_____.
【答案】96cm2
【解析】
首先根据题意画出图形,由菱形ABCD的周长是40cm,推出AB=BC=CD=DA=10cm,OA=OC,OB=OD,AC⊥BD,再由AC:BC=3:4,求出OA:OD=3:4后,设OA=3x, OD=4x, 根据勾股定理有![]() ,即可求得OA=6cm,OD=8cm,继而求出AC=12cm,BD=16cm,然后根据菱形的面积公式即可求出结果.
,即可求得OA=6cm,OD=8cm,继而求出AC=12cm,BD=16cm,然后根据菱形的面积公式即可求出结果.
解:如图,
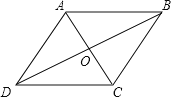
∵菱形ABCD的周长是40cm,
∴AB=BC=CD=DA=10cm,
∴OA=OC,OB=OD,AC⊥BD,
∵AC:BD=3:4,
∴OA:OD=3:4,
设OA=3x, OD=4x,
∵∠AOB=90°,
∴![]() ,
,
∴x=2(取正值)
∴OA=6cm,OD=8cm,
∴AC=12cm,BD=16cm,
∴S菱形ABCD=![]() =
=![]() =96cm2.
=96cm2.


科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=mx2﹣nx﹣m+n(m>0).
(Ⅰ)求证:该函数图象与x轴必有交点;
(Ⅱ)若m﹣n=3,
(ⅰ)当﹣m≤x<1时,二次函数的最大值小于0,求m的取值范围;
(ⅱ)点A(p,q)为函数y2=|mx2﹣nx﹣m+n|图象上的动点,当﹣4<p<﹣1时,点A在直线y=﹣x+4的上方,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点坐标为(2,﹣1)的抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点.
(1)求抛物线的表达式;
(2)设抛物线的对称轴与直线BC交于点D,连接AC、AD,求△ACD的面积;
(3)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与△BCO相似?若存在,求点E的坐标;若不存在,请说明理由.
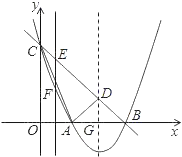
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马路两侧有两根灯杆AB、CD,当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长为NE,测得BD=24m,NB=6m,NE=2m.
(1)若小明的身高MN=1.6m,求AB的长;
(2)试判断这两根灯杆的高度是否相等,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
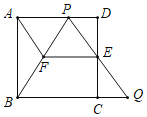
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,为放置在水平桌面![]() 上的台灯,底座的高
上的台灯,底座的高![]() 为
为![]() .长度均为
.长度均为![]() 的连杆
的连杆![]() ,
,![]() 与
与![]() 始终在同一水平面上.
始终在同一水平面上.
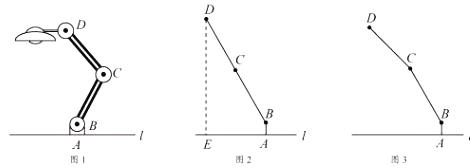
(1)旋转连杆![]() ,
,![]() ,使
,使![]() 成平角,
成平角,![]() ,如图2,求连杆端点
,如图2,求连杆端点![]() 离桌面
离桌面![]() 的高度
的高度![]() .
.
(2)将(1)中的连杆![]() 绕点
绕点![]() 逆时针旋转,使
逆时针旋转,使![]() ,如图3,问此时连杆端点
,如图3,问此时连杆端点![]() 离桌面
离桌面![]() 的高度是增加了还是减少?增加或减少了多少?(精确到
的高度是增加了还是减少?增加或减少了多少?(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD申CD边上任意一点.
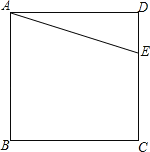
(1)以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形;
(2)在BC边上画一点F,使△CFE的周长等于正方形ABCD的周长的一半,请简要说明你取该点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com