
【题目】如图,BC是半圆的直径,点D是半圆上的一点,过D作圆O的切线AD,BA垂直DA于点A,BA交半圆于点E,已知BC=10,AD=4,那么直线CE与以点O为圆心、 ![]() 为半径的圆的位置关系是( )
为半径的圆的位置关系是( )
A.相切
B.相交
C.相离
D.无法确定
【答案】C
【解析】连接OD交CE于F,则OD⊥AD.
又∵BA⊥DA,
∴OD∥AB.
∵OB=OC,
∴CF=EF,
∴OD⊥CE,
则四边形AEFD是矩形,得EF=AD=4.
连接OE.
在Rt△OEF中,根据勾股定理得OF=3> ![]()
即圆心O到CE的距离大于圆的半径,则直线和圆相离,
故选C.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对直线与圆的三种位置关系的理解,了解直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.


科目:初中数学 来源: 题型:
【题目】世界杯决赛分成8个小组,每小组4个队,小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,选出2个队进入16强,胜一场得3分,平一场得1分,负一场得0分.
(1)求每小组共比赛多少场?
(2)在小组比赛中,现有一队得到6分,该队出线是一个确定事件,还是不确定事件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=x的图象为直线l.
(1)观察与探究
已知点A与A′,点B与B′分别关于直线l对称,其位置和坐标如图所示.请在图中标出C(4,﹣1)关于线l的对称点C′的位置,并写出C′的坐标_____;
(2)归纳与发现
观察以上三组对称点的坐标,你会发现:
平面直角坐标系中点P(a,b)关于直线l的对称点P′的坐标为_____;
(3)运用与拓展
已知两点M(﹣3,3)、N(﹣4,﹣1),试在直线l上作出点Q,使点Q到M、N两点的距离之和最小,并求出相应的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
思路:(1) 作AD⊥BC于D,设BD = x,用含x的代数式表示CD;(2)根据勾股定理,利用AD作为“桥梁”,建立方程模型,求出x;(3)利用勾股定理求出AD的长,再计算三角形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点(4,m)在反比例函数![]() (x≠0)的图象上,则m的值是 .
(x≠0)的图象上,则m的值是 .
【答案】2
【解析】∵点(4,m)在反比例函数y=![]() (x≠0)的图象上,
(x≠0)的图象上,
∴m=8÷4,解得m=2.
故答案为:2.
【题型】填空题
【结束】
12
【题目】如上图,反比例函数![]() 的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .
的图象位于第一、三象限,其中第一象限内的图象经过点A(1,2),请在第三象限内的图象上找一个你喜欢的点P,你选择的P点坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OC=5cm,直线l⊥OC,垂足为H,且l交⊙O于A、B两点,AB=8cm,求l沿OC所在直线向下平移多少cm时与⊙O相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, △P1OA1与△P2A1A2是等腰直角三角形,点![]() 、
、![]() 在函数
在函数![]() 的图象上,斜边
的图象上,斜边![]() 、
、![]() 都在
都在![]() 轴上,则点
轴上,则点![]() 的坐标是____________.
的坐标是____________.
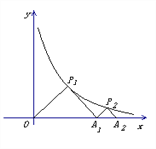
【答案】(![]() ,0)
,0)
【解析】因为△P1OA1是等腰直角三角形,所以设P1(a,a),则a2=4,a=2,所以OA1=2×2=4,又因为△P2A1A2是等腰直角三角形,设P2(4+b,b),所以b(4+b)=4,解得b=![]() ,所以A1A2=
,所以A1A2=![]() ,所以OA2=
,所以OA2=![]() +4=
+4=![]() ,则A2(
,则A2(![]() ,0),故答案为(
,0),故答案为(![]() ,0).
,0).
【题型】填空题
【结束】
16
【题目】如图,函数y=![]() 和y=
和y=![]() 在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________
在第一象限的图像,点P1,P2,P3,……,P2011都是曲线上的点,它们的横坐标分别为x1,x2,x3,……,x2011,纵坐标分别为1,3,5,7……,是连续的2011个奇数,过各个P点作y的平行线,与另一双曲线交点分别是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),……,Q2012(x2012,y2012),则y2012=___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图17-Z-11,小红同学要测量A,C两地的距离,但A,C之间有一水池,不能直接测量,于是她在A,C同一水平面上选取了一点B,点B可直接到达A,C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A,C两地之间的距离.(结果精确到1米,参考数据: ![]() ≈4.6)
≈4.6)
![]()
图17-Z-11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com