
分析 分类讨论,①点C在对称轴上,②开口向上,且AB=AC或AB=BC;③开口向下,且AB=AC或AB=BC;分别求出a的值即可解题.
解答 解:存在3种情况,①如图1,此时a>0,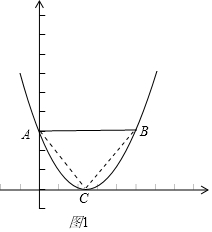
此时抛物线与x轴只有一个交点,AC=BC,
此时△=0,解得:a=$\frac{12}{25}$,(符合题意);
②此时AB=BC=5或AB=AC′=5,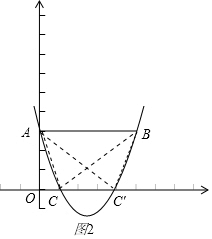
∵OA=3,∴此时点C坐标为(1,0)或(4,0),
带入C点坐标得:a=$\frac{3}{4}$;
③此时BC=AB=5或AB=AC′=5,此时a<0,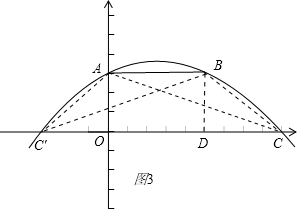
∵BD=AO=3,BC=5,∴CD=$\sqrt{{BC}^{2}{-BD}^{2}}$=4,
∴点C坐标为(9,0)或(-4,0),带入点C坐标得:a=-$\frac{1}{12}$,(符合题意)
故答案为 $\frac{12}{25}$或$\frac{3}{4}$或-$\frac{1}{12}$.
点评 本题考查了分类讨论思想,考查了代入法求抛物线解析式的方法,本题容易漏解,找到3种情况并分别求出a的值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
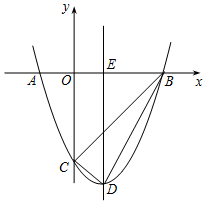 如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
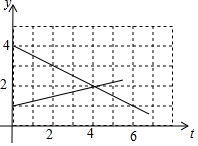 某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.
某工厂有甲、乙两个长方体的水池,甲水池较深,甲池的水用抽水机匀速地抽入乙池,如图所示的是甲、乙两个水池水的深度y(m)与抽水时间t(h)的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
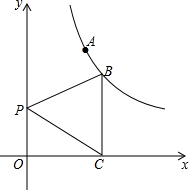 已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-4mx+4m+4(m≠0)的顶点为P.P,M两点关于原点O成中心对称.
在平面直角坐标系xOy中,抛物线y=mx2-4mx+4m+4(m≠0)的顶点为P.P,M两点关于原点O成中心对称.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com