
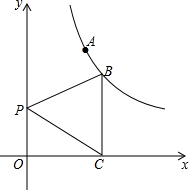
 已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
已知点A(1,2)、点 B在双曲线y=$\frac{k}{x}$(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,分析 (1)利用待定系数法即可求得k的值;设B的坐标是(m,n)则mn=2,BC=n,OC=m,利用三角形的面积公式求解;
(2)把y1和y2用x1和x2表示出来,然后求s-t的值,对式子进行变形判断s-t的符号即可.
解答 解:(1)把A(1,2)代入y=$\frac{k}{x}$得k=2;
设B的坐标是(m,n)则mn=2,BC=n,OC=m.
则S△PBC=$\frac{1}{2}$BC•OC=$\frac{1}{2}$mn=1;
(2)s>t;
理由:∵s-t═$\frac{{{x_1}+{x_2}}}{2}-\frac{4}{{{x_1}+{x_2}}}=\frac{{{x_1}+{x_2}}}{{{x_1}•{x_2}}}-\frac{4}{{{x_1}+{x_2}}}$=$\frac{{{y_1}+{y_2}}}{2}-\frac{4}{{{x_1}+{x_2}}}$
═$\frac{{\frac{2}{x_1}+\frac{2}{x_2}}}{2}-\frac{4}{{{x_1}+{x_2}}}$═$\frac{{{{({{x_1}+{x_2}})}^2}-4{x_1}•x}}{{{x_1}•{x_2}•({{x_1}+{x_2}})}}$=$\frac{{{{({{x_1}-{x_2}})}^2}}}{{{x_1}•{x_2}•({{x_1}+{x_2}})}}$,
∵x2>x1>0,∴${({{x_1}-{x_2}})^2}$>0,x1•x2•(x1+x2)>0,
∴$\frac{{{{({{x_1}-{x_2}})}^2}}}{{{x_1}•{x_2}•({{x_1}+{x_2}})}}>0$;
∴s>t.
点评 本题考查了待定系数法求反比例函数的解析式,以及比较分式的值的大小,常用的方法一般是转化为求差,判断差的符号解决.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 成本(万元/件) | 100 | 80 |
| 售价(万元/件) | 170 | 120 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
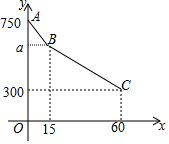 周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.
周末,小军在医院里照顾奶奶输液,小军问:“按照这样的输液速度,多少时间能结束输液?”护上答:“75分钟.”15分钟后,小军减慢了输液的速度,60分钟后,小军发现还剩有300毫升药液,剩下待输药液y(毫升)与输液时间x(分钟)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有最大值$\frac{a}{4}$ | B. | 有最大值-$\frac{a}{4}$ | C. | 有最小值$\frac{a}{4}$ | D. | 有最小值-$\frac{a}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com