
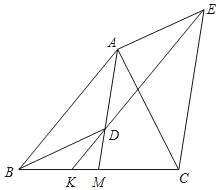
【题目】如图,AM是△ABC的中线,点D是线段AM上一点(不与点A重合).过点D作KD∥AB,交BC于点K,过点C作CE∥AM,交KD的延长线于点E,连接AE、BD.
(1)求证:△ABM∽△EKC;
(2)求证:ABCK=EKCM;
(3)判断线段BD、AE的关系,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)BD∥AE,BD=AE.理由见解析.
【解析】
(1)根据平行线的性质得到∠ABC=∠EKC,∠AMB=∠ECK,得到△ABM∽△EKC;
(2)根据相似三角形的性质得到比例式,计算即可;
(3)根据相似三角形的性质得到DE=AB,得到四边形ABDE是平行四边形,根据平行是四边形的性质解答.
(1)∵KD∥AB,
∴∠ABC=∠EKC,
∵CE∥AM,
∴∠AMB=∠ECK,
∴△ABM∽△EKC;
(2)∵△ABM∽△EKC,
∴![]() ,
,
∴ABCK=EKBM,
∵AM是△ABC的中线,
∴BM=CM,
∴ABCK=EKCM;
(3)解:BD∥AE,BD=AE,
∵CE∥AM,
∴![]() ,
,
∵![]() ,
,
∴DE=AB,
∵DE∥AB,
∴四边形ABDE是平行四边形,
∴BD∥AE,BD=AE.


科目:初中数学 来源: 题型:
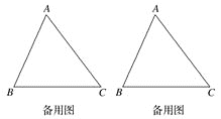
【题目】如图1,给定锐角三角形ABC,小明希望画正方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上,他发现直接画图比较困难,于是他先画了一个正方形HIJK,使得点H,I位于射线BC上,K位于射线BA上,而不需要求J必须位于AC上.这时他发现可以将正方形HIJK通过放大或缩小得到满足要求的正方形DEFG.
阅读以上材料,回答小明接下来研究的以下问题:
(1)如图2,给定锐角三角形ABC,画出所有长宽比为2:1的长方形DEFG,使D,E位于边BC上,F,G分别位于边AC,AB上.
(2)已知三角形ABC的面积为36,BC=12,在第(1)问的条件下,求长方形DEFG的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
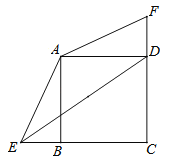
【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他各项费用80元.
销售单价x(元) | 3.5 | 5.5 |
销售量y(袋) | 280 | 120 |
(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
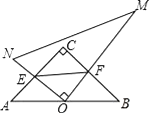
【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+
x2+ ![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
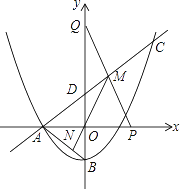
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴的一个交点为
轴的一个交点为![]()
![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,过
,过![]() 的直线为
的直线为![]() .
.
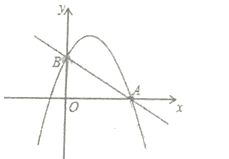
(1)求二次函数![]() 的解析式及点
的解析式及点![]() 的坐标;
的坐标;
(2)直接写出满足![]() 时,
时,![]() 的取值 ;
的取值 ;
(3)在两坐标轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,求出
为底边的等腰三角形?若存在,求出![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的甬江宛如一条玉带穿城而过,数学课外实践活动中,小林在甬江岸边的A, B两点处,利用测角仪分别对西岸的一观景亭D进行测量.如图,测得∠DAC=45°,∠DBC=65°,若AB=114米,求观景亭D到甬江岸边AC的距离约为多少米?
(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)
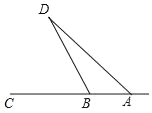
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com