
【题目】如图,抛物线y=![]() x2+
x2+ ![]() x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,
x+c与x轴的负半轴交于点A,与y轴交于点B,连结AB,点C(6,![]() )在抛物线上,直线AC与y轴交于点D.
)在抛物线上,直线AC与y轴交于点D.
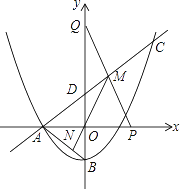
(1)求c的值及直线AC的函数表达式;
(2)点P在x轴正半轴上,点Q在y轴正半轴上,连结PQ与直线AC交于点M,连结MO并延长交AB于点N,若M为PQ的中点.
①求证:△APM∽△AON;
②设点M的横坐标为m,求AN的长(用含m的代数式表示).
【答案】(1)y=![]() x2+
x2+![]() x-3,y=
x-3,y=![]() x+3(2)AN=
x+3(2)AN=![]()
【解析】试题(1)把C点坐标代入抛物线解析式可求得c的值,令y=0可求得A点坐标,利用待定系数法可求得直线AC的函数表达式;
(2)①在Rt△AOB和Rt△AOD中可求得∠OAB=∠OAD,在Rt△OPQ中可求得MP=MO,可求得∠MPO=∠MOP=∠AON,则可证得△APM∽△AON;
②过M作ME⊥x轴于点E,用m可表示出AE和AP,进一步可表示出AM,利用△APM∽△AON可表示出AN.
(1)把C点坐标代入抛物线解析式可得![]() ,解得c=﹣3,∴抛物线解析式为
,解得c=﹣3,∴抛物线解析式为![]() ,令y=0可得
,令y=0可得![]() ,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式为y=kx+b(k≠0),把A、C坐标代入可得:
,解得x=﹣4或x=3,∴A(﹣4,0),设直线AC的函数表达式为y=kx+b(k≠0),把A、C坐标代入可得: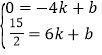 ,解得:
,解得: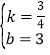 ,∴直线AC的函数表达式为
,∴直线AC的函数表达式为![]() ;
;
(2)①∵在Rt△AOB中,tan∠OAB=![]() =
=![]() ,在RtAOD中,tan∠OAD=
,在RtAOD中,tan∠OAD=![]() =
=![]() ,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
,∴∠OAB=∠OAD,∵在Rt△POQ中,M为PQ的中点,∴OM=MP,∴∠MOP=∠MPO,且∠MOP=∠AON,∴∠APM=∠AON,∴△APM∽△AON;
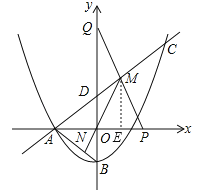
②如图,过点M作ME⊥x轴于点E,则OE=EP,∵点M的横坐标为m,∴AE=m+4,AP=2m+4,∵tan∠OAD=![]() ,∴cos∠EAM=cos∠OAD=
,∴cos∠EAM=cos∠OAD=![]() ,∴
,∴![]() =
=![]() ,∴AM=
,∴AM=![]() AE=
AE=![]() ,∵△APM∽△AON,∴
,∵△APM∽△AON,∴![]() ,即
,即![]() ,∴AN=
,∴AN=![]() .
.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
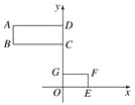
【题目】如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(-4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为( )
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.

(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
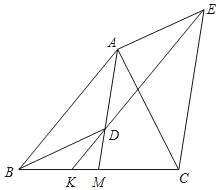
【题目】如图,AM是△ABC的中线,点D是线段AM上一点(不与点A重合).过点D作KD∥AB,交BC于点K,过点C作CE∥AM,交KD的延长线于点E,连接AE、BD.
(1)求证:△ABM∽△EKC;
(2)求证:ABCK=EKCM;
(3)判断线段BD、AE的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
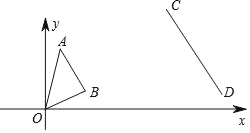
【题目】如图,平面直角坐标系中,A(1,4)、B(3,1)、C(9,7)、D(13,1),若以CD为边的三角形与△OAB位似,则这两个三角形的位似中心为( )
A. (0,0) B. (3,4)或(﹣6,2)
C. (5,3)或(-7,1) D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx+c(ab≠0)经过原点,顶点为A.
(1)若点A的坐标是(﹣2,﹣4),
①求抛物线的解析式;
②把抛物线在第三象限之间的部分图象记为图象G,若直线y=﹣x+n与图象G有两个不同的交点,求n的取值范围;
(2)若直线y2=ax+b经过点A,当1<x<2时,比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=﹣x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(﹣1,5),点A与y1的顶点B的距离是4.
(1)求y1的解析式;
(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
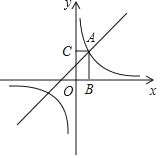
【题目】如图,已知点A(a,3)是一次函数y1=x+1与反比例函数y2=![]() 的图象的交点.(1)求反比例函数的解析式;(2)在y轴的右侧,当y1>y2时,直接写出x的取值范围;(3)求点A与两坐标轴围成的矩形OBAC的面积.
的图象的交点.(1)求反比例函数的解析式;(2)在y轴的右侧,当y1>y2时,直接写出x的取值范围;(3)求点A与两坐标轴围成的矩形OBAC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com