
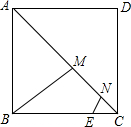
 如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为$\sqrt{2}$的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是$\frac{2}{3}$.
如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为$\sqrt{2}$的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是$\frac{2}{3}$. 分析 根据题意得出作EF∥AC且EF=$\sqrt{2}$,连结DF交AC于M,在AC上截取MN=$\sqrt{2}$,此时四边形BMNE的周长最小,进而利用相似三角形的判定与性质得出答案.
解答 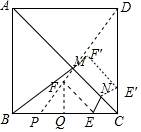 解:作EF∥AC且EF=$\sqrt{2}$,连结DF交AC于M,在AC上截取MN=$\sqrt{2}$,延长DF交BC于P,作FQ⊥BC于Q,作出点E关于AC的对称点E′,则CE′=CE=1,将MN平移至E′F′处,则四边形MNE′F′为平行四边形,
解:作EF∥AC且EF=$\sqrt{2}$,连结DF交AC于M,在AC上截取MN=$\sqrt{2}$,延长DF交BC于P,作FQ⊥BC于Q,作出点E关于AC的对称点E′,则CE′=CE=1,将MN平移至E′F′处,则四边形MNE′F′为平行四边形,
则当BM+EN=BM+FM=BF′时四边形BMNE的周长最小,
由∠FEQ=∠ACB=45°,可求得FQ=EQ=1,
∵∠DPC=∠FPQ,∠DCP=∠FQP,
∴△PFQ∽△PDC,
∴$\frac{PQ}{PQ+QE+EC}$=$\frac{FQ}{CD}$,
∴$\frac{PQ}{PQ+2}$=$\frac{1}{4}$,
解得:PQ=$\frac{2}{3}$,
∴PC=$\frac{8}{3}$,
由对称性可求得tan∠MBC=tan∠PDC=$\frac{\frac{8}{3}}{4}$=$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 此题主要考查了正方形的性质以及相似三角形的判定与性质,得出M,N的位置是解题关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
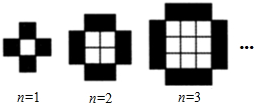 当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).
当白色小正方形个数n等于1,2,3,…时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第n个图形中白色小正方形的个数是n2和黑色小正方形的个数是4n(用n表示,n是正整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
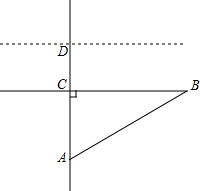 学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?
学校池塘的荷叶刚发新芽,如图中虚线所示,测得水深AC为0.6m,荷花根部与荷叶的水平距离CB为0.8m,且AD=AB,忽遇大雨,使池塘水位每小时上升0.1米,问3小时后荷叶是否有没顶之灾?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com