
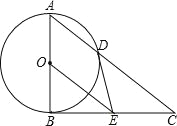
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心、OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=2CD·OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
【答案】(1)DE为⊙O的切线;证明见解析;(2)证明见解析;(3)![]()
【解析】
试题分析:(1)连接OD,BD,由AB为圆O的直径,得到∠ADB为直角,可得出三角形BCD为直角三角形,E为斜边BC的中点,利用斜边上的中线等于斜边的一半,得到CE=DE,利用等边对等角得到一对角相等,再由OA=OD,利用等边对等角得到一对角相等,由直角三角形ABC中两锐角互余,利用等角的余角相等得到∠ADO与∠CDE互余,可得出∠ODE为直角,即DE垂直于半径OD,可得出DE为圆O的切线;
(2)证明OE是△ABC的中位线,则AC=2OE,然后证明△ABC∽△BDC,根据相似三角形的对应边的比相等,即可证得;
(3)在直角△ABC中,利用勾股定理求得AC的长,根据三角形中位线定理OE的长即可求得.
试题分析:(1)连接OD,BD,
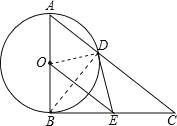
∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE=![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,即∠C+∠A=90°,
∴∠ADO+∠CDE=90°,即∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为⊙O的切线;
(2)∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴![]() ,即BC2=ACCD.
,即BC2=ACCD.
∴BC2=2CDOE;
(3)∵cos∠BAD=![]() ,
,
∴sin∠BAC=![]() ,
,
又∵BE=6,E是BC的中点,即BC=12,
∴AC=15.
又∵AC=2OE,
∴OE=![]() AC=
AC=![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+2x﹣3=0 时,方程变形正确的是_____(填序号)
①(x﹣1)2=2 ②(x+1)2=4 ③(x﹣1)2=1④(x+1)2=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
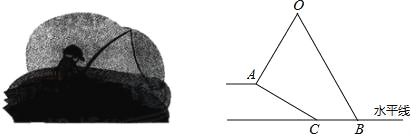
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长![]() 米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO的倾斜角是60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com