
如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=80,则∠ABC+∠BCD= ;∠E= ;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F所添加的条件为 .
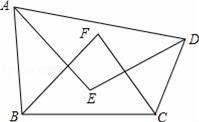

【考点】多边形内角与外角;三角形内角和定理.
【分析】(1)先根据三角形内角和定理求出∠FBC+∠BCF=180°﹣∠F=100°,再由角平分线定义得出∠ABC=2∠FBC,∠BCD=2∠BCF,那么∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;由四边形ABCD的内角和为360°,得出∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.由角平分线定义得出∠DAE=
 ∠BAD,∠ADE=
∠BAD,∠ADE=
 ∠CDA,那么∠DAE+∠ADE=
∠CDA,那么∠DAE+∠ADE=
 ∠BAD+
∠BAD+
 ∠CDA=
∠CDA=
 (∠BAD+∠CDA)=80°,然后根据三角形内角和定理求出∠E=180°﹣(∠DAE+∠ADE)=100°;
(∠BAD+∠CDA)=80°,然后根据三角形内角和定理求出∠E=180°﹣(∠DAE+∠ADE)=100°;
(2)由四边形ABCD的内角和为360°得到∠BAD+∠CDA+∠ABC+∠BCD=360°,由角平分线定义得出∠DAE+∠ADE+∠FBC+∠BCF=180°,又根据三角形内角和定理有∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,那么∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,于是∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)由(2)可知∠E+∠F=180°,如果∠E=∠F,那么可以求出∠E=∠F=90°,根据三角形内角和定理求出∠DAE+∠ADE=90°,再利用角平分线定义得到∠BAD+∠CDA=180°,于是AB∥CD.
【解答】解:(1)∵∠F=80,
∴∠FBC+∠BCF=180°﹣∠F=100°.
∵∠ABC、∠BCD的角平分线交于点F,
∴∠ABC=2∠FBC,∠BCD=2∠BCF,
∴∠ABC+∠BCD=2∠FBC+2∠BCF=2(∠FBC+∠BCF)=200°;
∵四边形ABCD的内角和为360°,
∴∠BAD+∠CDA=360°﹣(∠ABC+∠BCD)=160°.
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,
∴∠DAE=
 ∠BAD,∠ADE=
∠BAD,∠ADE=
 ∠CDA,
∠CDA,
∴∠DAE+∠ADE=
 ∠BAD+
∠BAD+
 ∠CDA=
∠CDA=
 (∠BAD+∠CDA)=80°,
(∠BAD+∠CDA)=80°,
∴∠E=180°﹣(∠DAE+∠ADE)=100°;
(2)∠E+∠F=180°.理由如下:
∵∠BAD+∠CDA+∠ABC+∠BCD=360°,
∵四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F,
∴∠DAE+∠ADE+∠FBC+∠BCF=180°,
∵∠DAE+∠ADE+∠E=180°,∠FBC+∠BCF+∠F=180°,
∴∠DAE+∠ADE+∠E+∠FBC+∠BCF+∠F=360°,
∴∠E+∠F=360°﹣(∠DAE+∠ADE+∠FBC+∠BCF)=180°;
(3)AB∥CD.
故答案为200°;100°;AB∥CD.
【点评】本题考查了三角形、四边形内角和定理,角平分线定义,平行线的判定,等式的性质,利用数形结合,理清角度之间的关系是解题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com