
如图,在△ABC中,沿DE折叠,点A落在三角形所在的平面内的点为A1,若∠A=30°,∠BDA1=80°,则∠CEA1的度数为 .
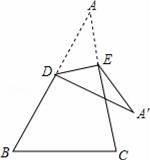

20°【考点】翻折变换(折叠问题).
【分析】由∠BDA1=80°,可知邻补角的度数,根据折叠的性质知∠ADE=∠A1DE,又∠A=30°,运用三角形的外角和求出∠DEC=80°,再根据邻补角定义和折叠的性质知∠AED=∠A1ED=100°,从而∠CEA1=∠A1ED﹣∠DEC=20°.
【解答】解:∵∠BDA1=80°,
∴∠ADA1=100°,
根据折叠的性质知∠ADE=∠A1DE=
 ,∠ADA1=50°,
,∠ADA1=50°,
又∵∠A=30°,
∴∠DEC=80°,
∴∠AED=∠A1ED=100°,
∴∠CEA1=∠A1ED﹣∠DEC=20°.
故答案为:20°.
【点评】本题考查了翻折变换(折叠问题)、三角形内角和及角的和差,熟悉折叠的性质是解决问题的关键.折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,
后面的每个数与它的前面一个数的差都是一个相等的常数,具有这种规律的一列数,除
了直接相加外,我们还可以用下列公式来求和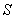 ,
, (其中
(其中 表示数的个
表示数的个
数,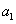 表示第一个数,
表示第一个数,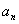 表示最后一个数).所以,
表示最后一个数).所以,
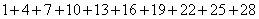 =
=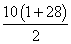
 .
.
用上面的知识解答下面问题:
某公司对外招商承包一个分公司,符合条件的两个企业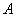 、
、 分别拟定上缴利润方案
分别拟定上缴利润方案
如下:
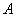 :每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元;
:每年结算一次上缴利润,第一年上缴1.5万元,以后每年比前一年增加1万元;
 :每半年结算一次上缴利润,第一个半年上缴0.3万元,以年每半年比前半年增加0.3万元.
:每半年结算一次上缴利润,第一个半年上缴0.3万元,以年每半年比前半年增加0.3万元.
(1)如果承包期限2年,则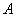 企业上缴利润的总金额为 万元,
企业上缴利润的总金额为 万元, 企业上缴利润的总金额为 万元;
企业上缴利润的总金额为 万元;
(2)如果承包期限为 年,则
年,则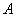 企业上缴利润的总金额为 万元,
企业上缴利润的总金额为 万元, 企业上缴利润
企业上缴利润
的总金额为 万元(用含 的代数式表示);
的代数式表示);
(3)承包期限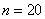 时,通过计算说明哪个企业上缴利润的总金额比较多?多多少万元?
时,通过计算说明哪个企业上缴利润的总金额比较多?多多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
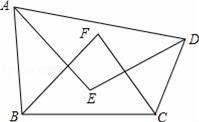
如图,四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E,∠ABC、∠BCD的角平分线交于点F.
(1)若∠F=80,则∠ABC+∠BCD= ;∠E= ;
(2)探索∠E与∠F有怎样的数量关系,并说明理由;
(3)给四边形ABCD添加一个条件,使得∠E=∠F所添加的条件为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com