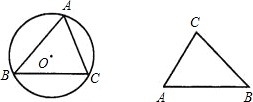解:(1)如图,设正方形的边长为a,
∵正方形的对边MN∥PQ,
∴△AMN∽△ABC,
∴

=

,
即

=

,
解得a=12,
∴这个正方形的面积=a
2=12
2=144;

(2)当PQ在BC上时,∵MN∥PQ,
∴△AMN∽△ABC,
∴

=

,
即

=

,
解得x=7.5,
∴①PQ在△ABC内部时,0<x≤7.5,重叠部分的面积为矩形MNPQ的面积,
y=x•2x=2x
2,
②PQ在△ABC外部时,7.5<x<30,设矩形MNPQ在△ABC内部的长为b,
∵△AMN∽△ABC,
∴

=
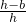
,
即

=

,
解得b=20-

x,
∴y=x(20-

x)=-

x
2+20x,
综上所述,y与x的关系式为y=

.
分析:(1)设正方形的边长为a,根据根据相似三角形对应高的比等于相似比列出比例式求解得到a,再根据正方形的面积公式计算即可得解;
(2)先根据相似三角形对应高的比等于相似比列式求出QP在BC上时的x的值,然后分①PQ在△ABC内部时,重叠部分的面积为矩形MNPQ的面积;②PQ在△ABC外部时,设矩形MNPQ在△ABC内部的长为b,根据相似三角形对应高的比等于相似比列出比例式求解得到b,再根据矩形的面积列式整理得到y与x的关系式.
点评:本题考查了相似三角形的判定与性质,矩形的对边平行且相等,正方形的对边平行且相等的性质,根据相似三角形的对应高的比等于对应边的比列出比例式是解题的关键.


 =
= ,
, =
= ,
,
 =
= ,
, =
= ,
, =
=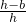 ,
, =
= ,
, x,
x, x)=-
x)=- x2+20x,
x2+20x, .
.

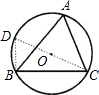 阅读材料,解答问题:
阅读材料,解答问题: