
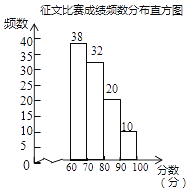
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
【答案】(1)0.2;(2)补全征文比赛成绩频数分布直方图见解析;(3)全市获得一等奖征文的篇数为300篇.
【解析】(1)由频率之和为1,用1减去其余各组的频率即可求得c的值;
(2)由频数分布表可知 60≤m<70的频数为:38,频率为:0.38,根据总数=频数÷频率得样本容量,再由频数=总数×频率求出a、b的值,根据a、b的值补全图形即可;
(3)由频数分布表可知评为一等奖的频率为:0.2+0.1=0.3,再用总篇数×一等奖的频率=全市一等奖征文篇数.
(1)c=1-0.38-0.32-0.1=0.2,
故答案为:0.2;
(2)38÷0.38=100,a=100×0.32=32,b=100×0.2=20,
补全征文比赛成绩频数分布直方图如图所示:
(3)由频数分布表可知评为一等奖的频率为:0.2+0.1=0.3,
∴全市获得一等奖征文的篇数为:1000×0.3=300(篇),
答:全市获得一等奖征文的篇数为300篇.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
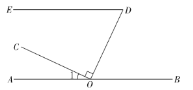
【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:![]() 和完全平方公式:
和完全平方公式:![]() 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式![]()
![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()

![]()
![]() .
.
根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将![]() 化成
化成![]() 的形式为_______;
的形式为_______;
(2)请你利用上述方法因式分解:
①![]() ; ②
; ②![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
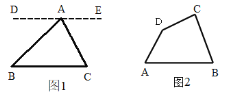
【题目】(1)我们知道“三角形三个内角的和为 180°”.现在我们用平行线的性质来证明这个结论是正确的.
已知:∠BAC、∠B、∠C 是△ABC 的三个内角,如图 1.
求证:∠BAC+∠B+∠C=180° 证明:过点 A 作直线 DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图 2,已知四边形 ABCD,求∠A+∠B+∠C+∠D 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )

A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.
问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.
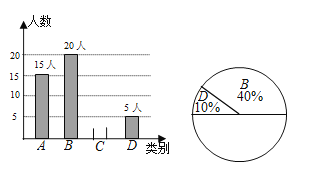
请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;补全条形统计图;
(2)求出C类人数占总调查人数的百分比及扇形统计图中![]() 类所对应扇形圆心角的度数.
类所对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐上,且点A(0,2),点C(![]() ,0),如图所示:抛物线
,0),如图所示:抛物线![]() 经过点B。
经过点B。
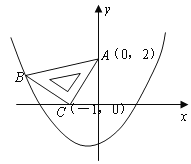
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com