
【题目】(1)我们知道“三角形三个内角的和为 180°”.现在我们用平行线的性质来证明这个结论是正确的.
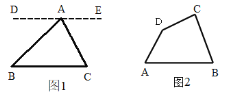
已知:∠BAC、∠B、∠C 是△ABC 的三个内角,如图 1.
求证:∠BAC+∠B+∠C=180° 证明:过点 A 作直线 DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图 2,已知四边形 ABCD,求∠A+∠B+∠C+∠D 的度数.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】将自然数按以下规律排列:

表中数2在第二行第一列,与有序数对(2,1)对应,数5与(1,3)对应,数14与(3,4)对应,根据这一规律,数2014对应的有序数对为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
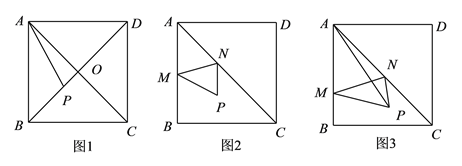
【题目】问题探究:在边长为![]() 的正方形
的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .
.
探究![]() :如图
:如图![]() ,若点
,若点![]() 是对角线
是对角线![]() 上任意一点,则线段
上任意一点,则线段![]() 的长的取值范围是__________;
的长的取值范围是__________;
探究![]() :如图
:如图![]() ,若点
,若点![]() 是
是![]() 内任意一点,点
内任意一点,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的值在探究
的值在探究![]() 中的取值范围内变化时,
中的取值范围内变化时, ![]() 的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出![]() 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;
问题解决:如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在面积为3的△ABC中,AB=3,∠BAC=45°,点D是BC边上一点.
(1)若AD是BC边上的中线,求AD的长;
(2)点D关于直线AB和AC的对称点分别为点M、N,求AN的长度的最小值;
(3)若P是△ABC内的一点,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1, ![]() ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2![]() 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.

A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com