
【题目】如图1,点![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,
上一点,![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)求![]() 的度数;
的度数;
(2)如图2,连接![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
求证:![]() .
.
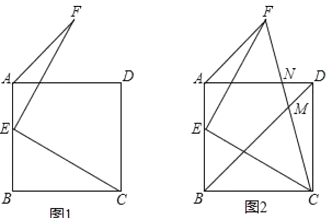
【答案】(1)135°;(2)见详解.
【解析】
(1)过点F作FM⊥AB交AB的延长线于点M,证明△EBC△FME,即可解决问题;
(2)过点F作FG//AB交BD于点G.先证明四边形ABGF为平行四边形,再证明△FGM△CDM,即可解决问题.
(1)过点F作FM⊥AB交AB的延长线于点M,
∵四边形ABCD是正方形,
∴∠B=∠M=∠CEF=90°,
∴∠MEF+∠CEB=90°,∠CEB+∠BCE=90°,
∴∠MEF=∠ECB,
∵EC=EF,
∴△EBC△FME(AAS) ,
∴FM=BE,EM=BC,
∵BC=AB,
∴EM=AB,
∴EMAE=ABAE,
∴AM=BE,
∴FM=AM,
∵FM⊥AB,
∴∠MAF=45°,
∴∠EAF=135°;
(2)过点F作FG//AB交BD于点G.
由(1)可知∠EAF=135°,
∵∠ABD=45°,
∴∠EAF+∠ABD=180°,
∴AF//BG,
∵FG//AB,
∴四边形ABGF为平行四边形,
∴AF=BG,FG=AB,
∵AB=CD,
∴FG=CD,
∵AB//CD,
∴FG//CD,
∴∠FGM=∠CDM,
∵∠FMG=∠CMD
∴△FGM△CDM(AAS),
∴GM=DM,
∴DG=2DM,
∴BD=BG+DG=AF+2DM.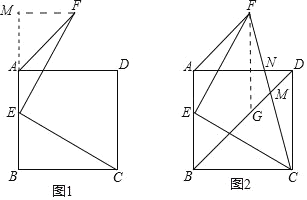


科目:初中数学 来源: 题型:
【题目】将正方形ABCD(如图1)作如下划分:第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH按上述方法再作划分,得图3,则图3中共有_________个正方形;若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有_______个正方形;继续划分下去,能否将正方形ABCD划分成有2011个正方形的图形?需说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我们知道“三角形三个内角的和为 180°”.现在我们用平行线的性质来证明这个结论是正确的.
已知:∠BAC、∠B、∠C 是△ABC 的三个内角,如图 1.
求证:∠BAC+∠B+∠C=180° 证明:过点 A 作直线 DE∥BC(请你把证明过程补充完整)
(2)请你用(1)中的结论解答下面问题:
如图 2,已知四边形 ABCD,求∠A+∠B+∠C+∠D 的度数.
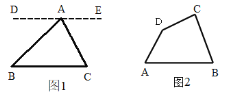
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )

A. 115°B. 125°C. 135°D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB=AC=10,BC=12,P是![]() 上的一个动点,过点P作BC的平行线交AB的延长线于点D.
上的一个动点,过点P作BC的平行线交AB的延长线于点D.
(1)当点P在什么位置时,DP是⊙O的切线?请说明理由;
(2)当DP为⊙O的切线时,求线段DP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.
问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.
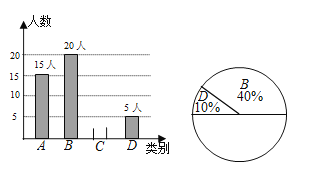
请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;补全条形统计图;
(2)求出C类人数占总调查人数的百分比及扇形统计图中![]() 类所对应扇形圆心角的度数.
类所对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com