
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:

(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
【答案】(1)y=-x+180;(2)售价定为140元/件时,每天最大利润W=1600元.
【解析】(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于kb的关系式,求出k、b的值即可;
(2)把每天的利润W与销售单价x之间的函数关系式化为二次函数顶点式的形式,由此关系式即可得出结论.
解:(1)设y与x之间的函数关系式为y=kx+b(k≠0),由所给函数图象可知,
![]() ,解得
,解得![]() .
.
故y与x的函数关系式为y=﹣x+180;
(2)∵y=﹣x+180,
∴W=(x﹣100)y=(x﹣100)(﹣x+180)
=﹣x2+280x﹣18000
=﹣(x﹣140)2+1600,
∵a=﹣1<0,
∴当x=140时,W最大=1600,
∴售价定为140元/件时,每天最大利润W=1600元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
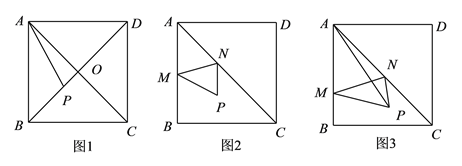
【题目】问题探究:在边长为![]() 的正方形
的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .
.
探究![]() :如图
:如图![]() ,若点
,若点![]() 是对角线
是对角线![]() 上任意一点,则线段
上任意一点,则线段![]() 的长的取值范围是__________;
的长的取值范围是__________;
探究![]() :如图
:如图![]() ,若点
,若点![]() 是
是![]() 内任意一点,点
内任意一点,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的值在探究
的值在探究![]() 中的取值范围内变化时,
中的取值范围内变化时, ![]() 的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出![]() 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;
问题解决:如图![]() ,在边长为
,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 是
是![]() 内任意一点,且
内任意一点,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 边和对角线
边和对角线![]() 上的两个动点,则当
上的两个动点,则当![]() 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角三角形ABC内接于⊙O,AD⊥BC,垂足为D.
(1)如图1, ![]() ,BD=DC,求∠B的度数;
,BD=DC,求∠B的度数;
(2)如图2,BE⊥AC,垂足为E,BE交AD于点F,过点B作BG∥AD交⊙O于点G,在AB边上取一点H,使得AH=BG.求证:△AFH是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误结论有( );①三角形三条高(或高的延长线)的交点不在三角形的内部,就在三角形的外部;②一个多边形的边数每增加一条,这个多边形的内角和就增加360;③两条平行直线被第三条直线所截,同旁内角的角平分线互相平行;④三角形的一个外角等于任意两个内角的和;⑤在![]() 中,若
中,若![]() ,则
,则![]() 为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
为直角三角形;⑥顺次延长三角形的三边,所得的三角形三个外角中锐角最多有一个
A. 6个B. 5个C. 4个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是菱形,且∠ABC=60,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则下列五个结论中正确的是( )
①若菱形ABCD的边长为1,则AM+CM的最小值1;
②△AMB≌△ENB;
③S四边形AMBE=S四边形ADCM;
④连接AN,则AN⊥BE;
⑤当AM+BM+CM的最小值为2![]() 时,菱形ABCD的边长为2.
时,菱形ABCD的边长为2.

A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com