
【题目】如图,在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上,△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ![]() ,
, ![]() ),那么点A3的纵坐标是 , 点An的纵坐标是 .
),那么点A3的纵坐标是 , 点An的纵坐标是 . 
【答案】![]() ;(
;( ![]() )n﹣1
)n﹣1
【解析】解:∵A1(1,1),A2( ![]() ,
, ![]() )在直线y=kx+b上,
)在直线y=kx+b上,
∴ 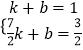 ,
,
解得 ![]() ,
,
∴直线解析式为:y= ![]() x+
x+ ![]() ;
;
设直线与x轴、y轴的交点坐标分别为N、M,
当x=0时,y= ![]() ,
,
当y=0时, ![]() x+
x+ ![]() =0,
=0,
解得x=﹣4,
∴点M、N的坐标分别为M(0, ![]() ),N(﹣4,0),
),N(﹣4,0),
∴tan∠MNO= ![]() =
= ![]() =
= ![]() ,
,
作A1C1⊥x轴与点C1 , A2C2⊥x轴与点C2 , A3C3⊥x轴与点C3 ,
∵A1(1,1),A2( ![]() ,
, ![]() ),
),
∴OB2=OB1+B1B2=2×1+2× ![]() =2+3=5,
=2+3=5,
tan∠MNO= ![]() =
= ![]() =
= ![]() ,
,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3 ,
∴A3C3= ![]() =(
=( ![]() )2 ,
)2 ,
同理可求,第四个等腰直角三角形A4C4= ![]() =(
=( ![]() )3 ,
)3 ,
依此类推,点An的纵坐标是( ![]() )n﹣1 ,
)n﹣1 ,
所以答案是: ![]() ,(
,( ![]() )n﹣1 .
)n﹣1 . 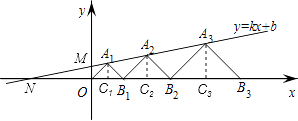
【考点精析】解答此题的关键在于理解数与式的规律的相关知识,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为 ![]() ,则a、b的值分别为( )
,则a、b的值分别为( ) 
A.![]() ,
, ![]()
B.![]() ,﹣
,﹣ ![]()
C.![]() ,﹣
,﹣ ![]()
D.﹣ ![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°, ![]() =
= ![]() ,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )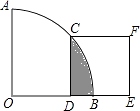
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=45°,∠ACB=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,点F在线段AG上,延长DA至点E,使AE=AF,连接EG,CG,DF,若EG=DF,点G在AC的垂直平分线上,则 ![]() 的值为
的值为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在ABCD中,对角线AC与BD相交于点O,经过点O的直线与边AB相交于点E,与边CD相交于点F. 
(1)求证:OE=OF;
(2)如图2,连接DE,BF,当DE⊥AB时,在不添加其他辅助线的情况下,直接写出腰长等于 ![]() BD的所有的等腰三角形.
BD的所有的等腰三角形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示. 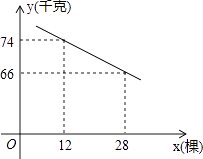
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对△ABC纸片进行如下操作: 第1次操作:将△ABC沿着过AB中点D1的直线折叠,使点A落在BC边上的A1处,折痕D1E1到BC的距离记作h1 , 然后还原纸片;
第2次操作:将△AD1E1沿着过AD1中点D2的直线折叠,使点A落在D1E1边上的A1处,折痕D1E1到BC的距离记作h2 , 然后还原纸片;
…
按上述方法不断操作下去…,经过第n次操作后得到的折痕DnEn到BC的距离记作hn , 若h=1,则hn的值不可能是( )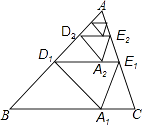
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,李玉刚同学随爸爸妈妈回老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km.设爸爸骑行时间为x(h).
(1)请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;
(2)请在同一个平面直角坐标系中画出(1)中两个函数的图象;
(3)请回答谁先到达老家.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=x2+(1﹣m)x﹣m(其中0<m<1)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC
(1)∠ABC的度数为
(2)求P点坐标(用含m的代数式表示)
(3)在坐标轴上是否存在着点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com