
【题目】如图,在扇形AOB中,∠AOB=90°, ![]() =
= ![]() ,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )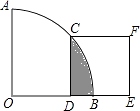
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
【答案】A
【解析】解:连接OC,如图所示:
∵在扇形AOB中∠AOB=90°, ![]() =
= ![]() ,
,
∴∠COD=45°,
∴OD=CD,
∴OC= ![]() =4,
=4,
∴阴影部分的面积=扇形BOC的面积﹣△ODC的面积
= ![]() ﹣
﹣ ![]() ×(2
×(2 ![]() )2=2π﹣4.
)2=2π﹣4.
故选:A.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形,以及对扇形面积计算公式的理解,了解在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,点F是⊙O与AB的一个交点,连接DF并延长交CB的延长线于点G,则BG的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题: 
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程 ①构造函数,画出图象:
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;
②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集. ①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题: 
(1)猜想△CMN的形状,并证明你的结论;
(2)请你证明CN是⊙O的切线;
(3)若等边△ABC的边长是2,求ADAM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,则下列结论中错误的是( ) 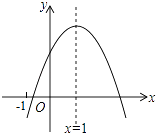
A.abc<0
B.a﹣b+c<0
C.b2﹣4ac>0
D.3a+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.
(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元. ①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y=kx+b和x轴上,△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形,如果A1(1,1),A2( ![]() ,
, ![]() ),那么点A3的纵坐标是 , 点An的纵坐标是 .
),那么点A3的纵坐标是 , 点An的纵坐标是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com