
【题目】抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,与y轴交于点C,点B,C的坐标分别为(4,0)和(0,4),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
(1)求抛物线和直线AD的解析式;
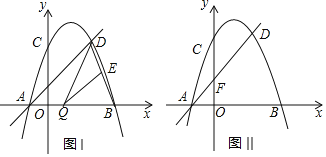
(2)如图Ⅰ,点Q是线段AB上一动点,过点Q作QE∥AD,交BD于点E,连接DQ,求△QED面积的最大值;
(3)如图Ⅱ,直线AD交y轴于点F,点M,N分别是抛物线对称轴和抛物线上的点,若以C,F,M,N为顶点的四边形是平行四边形,求点M的坐标.
【答案】(1)y=﹣![]() x2+x+4,y=x+2;(2)△QED面积的最大值是3;(3)点M的坐标为(1,
x2+x+4,y=x+2;(2)△QED面积的最大值是3;(3)点M的坐标为(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() ).
).
【解析】
(1)待定系数法得到抛物线的解析式为y=﹣![]() x2+x+4;直线AD的解析式为y=x+2;
x2+x+4;直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),根据相似三角形的性质得到EG=![]() ,
,
∴S△QDE=S△BDQ﹣S△BEQ=![]() ×(4﹣m)×4﹣
×(4﹣m)×4﹣![]() (4﹣m)×
(4﹣m)×![]() =﹣
=﹣![]() m2+
m2+![]() m+
m+![]() ,根据二次函数的性质可求△QED面积的最大值;
,根据二次函数的性质可求△QED面积的最大值;
(3)分两种情况讨论①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,于是可求点M的坐标;
②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,求出点P、N的坐标后可求点M的坐标.
解:(1)根据题意得,
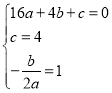 ,
,
解得: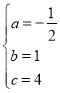 ,
,
∴抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
∵B(4,0),对称轴为x=1,
∴A(﹣2,0),
∵D(2,m)在抛物线的解析式y=﹣![]() x2+x+4上,
x2+x+4上,
∴点D的坐标是D(2,4),
设直线AD的解析式为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=x+2;
(2)如图1,作EG⊥x轴,设Q(m,0),
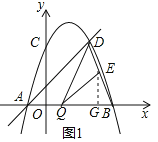
∵QE∥AD,
∴△BEQ∽△BDA,
∴![]() ,
,
即![]() ,
,
解得:EG=![]() ,
,
∴S△BEQ=![]() ×(4﹣m)×
×(4﹣m)×![]() ,
,
∴S△QDE=S△BDQ﹣S△BEQ=![]() ×(4﹣m)×4﹣
×(4﹣m)×4﹣![]() (4﹣m)×
(4﹣m)×![]() =﹣
=﹣![]() m2+
m2+![]() m+
m+![]() =﹣
=﹣![]() (m﹣1)2+3,
(m﹣1)2+3,
∴当m=1时,△QED面积取得最大值等于3;
(3)∵直线AD交y轴于点F,
∴F(0,2),
∵抛物线的解析式是y=﹣![]() x2+x+4上,
x2+x+4上,
∵抛物线的顶点坐标(1,![]() ),
),
①如图2,若CF为平行四边形的一边,则点N于抛物线的顶点重合,此时,MN=CF=2,
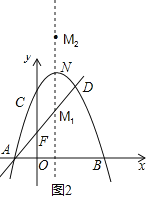
∴点M的坐标(1,![]() ),(1,
),(1,![]() );
);
②如图3,若CF为平行四边形的一条对角线,则CF与MN互相平分,
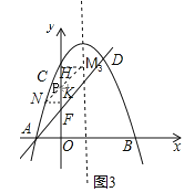
过点M,N分别向x轴作垂线,垂足分别为H,K,MN与HK交于点P,
易得△MHP≌△NKP,P(0,3)
∴点M,N的横坐标分别是1,﹣1,
∴N(﹣1,![]() ),
),
∴PK=3-![]() =
=![]() =HP,
=HP,
∴HO=3+![]() =
=![]() ,
,
∴M(1,![]() ),
),
综上所述,点M的坐标为:(1,![]() )或(1,
)或(1,![]() )或(1,
)或(1,![]() ).
).


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
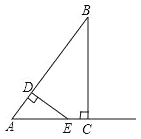
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,西藏日喀则市谢通门县发生了
日,西藏日喀则市谢通门县发生了![]() 级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
级地震,某校九年班、九年二班两班的班长交流了为地震灾区捐款的情况:
(1)九年一班班长说:“我们班捐款总额为![]() 元,我们班人数比你们班多
元,我们班人数比你们班多![]() 人”.
人”.
(2)九年二班班长说:“我们班捐款总额也为![]() 元,我们班人均捐款比你们班人均捐款多
元,我们班人均捐款比你们班人均捐款多![]() ”.
”.
请根据两个班长的对话,求这两个班级每班的人均捐款数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本
(1)求每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组经过市场调查,整理出某种商品在第![]() 天的售价与销量的相关信息如下表:
天的售价与销量的相关信息如下表:
观察表格:根据表格解答下列问题:
| 0 | 1 | 2 |
| 1 | ||
| -3 | -3 |
(1)![]() __________.
__________.![]() _____________.
_____________.![]() ___________.
___________.
(2)在下图的直角坐标系中画出函数![]() 的图象,并根据图象,直接写出当
的图象,并根据图象,直接写出当![]() 取什么实数时,不等式
取什么实数时,不等式![]() 成立;
成立;
(3)该图象与![]() 轴两交点从左到右依次分别为
轴两交点从左到右依次分别为![]() 、
、![]() ,与
,与![]() 轴交点为
轴交点为![]() ,求过这三个点的外接圆的半径.
,求过这三个点的外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
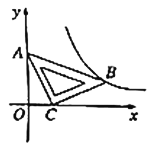
【题目】在平面直角坐标系![]() 中,将一块含有
中,将一块含有![]() 角的直角三角板如图放置,直角顶点
角的直角三角板如图放置,直角顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 恰好落在第一象限的双曲线上,现将直角三角板沿
恰好落在第一象限的双曲线上,现将直角三角板沿![]() 轴正方向平移,当顶点
轴正方向平移,当顶点![]() 恰好落在该双曲线上时停止运动,则此时点
恰好落在该双曲线上时停止运动,则此时点![]() 的对应点
的对应点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
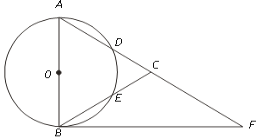
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com