
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
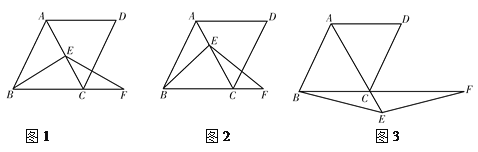
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
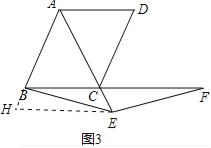
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
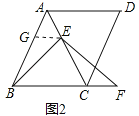
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
试题(1)根据菱形的性质证明△ABC是等边三角形和AB=2,求出△ABC的面积;
(2)作EG∥BC交AB于G,证明△BGE≌△ECF,得到BE=EF;
(3)作EH∥BC交AB的延长线于H,证明△BHE≌△ECF,得到BE=EF.
解:(1)∵四边形ABCD是菱形,∠ABC=60°,
∴△ABC是等边三角形,又E是线段AC的中点,
∴BE⊥AC,AE=AB=1,
∴BE=,
∴△ABC的面积=×AC×BE=;
(2)如图2,作EG∥BC交AB于G,
∵△ABC是等边三角形,
∴△AGE是等边三角形,
∴BG=CE,
∵EG∥BC,∠ABC=60°,
∴∠BGE=120°,
∵∠ACB=60°,
∴∠ECF=120°,
∴∠BGE=∠ECF,
在△BGE和△ECF中,
![]() ,
,
∴△BGE≌△ECF,
∴EB=EF;
(3)成立,
如图3,作EH∥BC交AB的延长线于H,
∵△ABC是等边三角形,
∴△AHE是等边三角形,
∴BH=CE,
在△BHE和△ECF中,
![]() ,
,
∴△BHE≌△ECF,
∴EB=EF.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
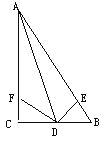
【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
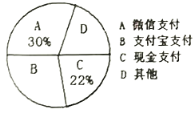
【题目】近几年居民购物的支付方式日益增多,为了解居民的支付习惯,七年级数学兴趣小组的学生利用课余时间在超市收银处进行了调查统计(每人只能选择其中一种方式支付),并将统计后的数据整理后绘制成如下不完整的两幅统计图,请根据图中有关信息解答下列问题:
各种支付方式的扇形统计图
各种支付方式的条形统计图
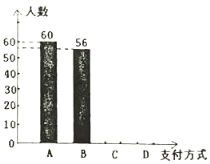
(1)本次共调查统计了多少人?
(2)![]() 支付宝支付占所调查人数的百分比是多少?
支付宝支付占所调查人数的百分比是多少?![]() 现金支付的居民有多少人?
现金支付的居民有多少人?
(3)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABE中,∠BAE=105°,AE的垂直平分线MN交BE于点C,且AB=CE,则∠B的度数是( )

A. 45°B. 60°C. 50°D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)请判断BD、CE有何大小、位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
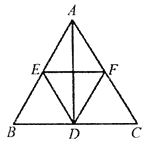
【题目】在![]() 中,D,E,F分别是三边
中,D,E,F分别是三边![]() ,
,![]() ,
,![]() 上的中点,连接
上的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,已知
,已知![]() .
.
(1)观察猜想:如图,当![]() 时,①四边形
时,①四边形![]() 的对角线
的对角线![]() 与
与![]() 的数量关系是________;②四边形
的数量关系是________;②四边形![]() 的形状是_______;
的形状是_______;

(2)数学思考:如图,当![]() 时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
时,(1)中的结论①,②是否发生变化?若发生变化,请说明理由;
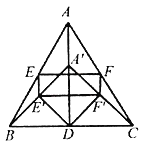
(3)拓展延伸:如图,将上图的点A沿![]() 向下平移到
向下平移到![]() 点,使得
点,使得![]() ,已知
,已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求四边形
的中点,求四边形![]() 与四边形
与四边形![]() 的面积比.
的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,AD∥BC,∠ABC=90o,AB=BC,点E是AB上的点,∠ECD=45o,连接ED,过D作DF⊥BC于F.

(1)若∠BEC=75o,FC=4,求梯形ABCD的周长。(4分)
(2)求证:ED=BE+FC.(6分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小刚相约周末到雪莲大剧院看演出,他们的家分别距离剧院1200m和2000m,两人分别从家中同时出发,已知小明和小刚的速度比是3:4,结果小明比小刚提前4min到达剧院.求两人的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com