
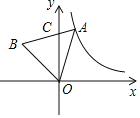
【题目】如图,等边![]() 的边
的边![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 图像上的一点,且
图像上的一点,且![]() ,则等边
,则等边![]() 的边长为______.
的边长为______.
【答案】![]()
【解析】
设等边三角形的边长为b,过点A作x轴的平行线交y轴于点M,设AM=a
过点B作y轴的平行线交AM的延长线于点E,过点O作ON⊥AB与点N,AN=![]() AB=
AB=![]() b,ON=
b,ON=![]() b,AN=
b,AN=![]() b,AC=
b,AC=![]() b,则CN=AN-AC=
b,则CN=AN-AC=![]() b,CM∥BE,则
b,CM∥BE,则![]() ,则
,则 ,则AE=3a,可证△ONC∽△AEB,
,则AE=3a,可证△ONC∽△AEB,![]() ,即
,即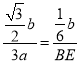 ,解得:BE=
,解得:BE=![]() ,AB2=AE2+BE2,则b2=
,AB2=AE2+BE2,则b2=![]() a2+9a2=
a2+9a2=![]() a2,点A(a,
a2,点A(a,![]() ),则AB2=a2+
),则AB2=a2+![]() ,即可求解.
,即可求解.
设等边三角形的边长为b,过点A作x轴的平行线交y轴于点M,设AM=a
过点B作y轴的平行线交AM的延长线于点E,过点O作ON⊥AB与点N,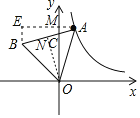
则AN=![]() AB=
AB=![]() b,ON=
b,ON=![]() b,AC=
b,AC=![]() b,
b,
则CN=AN-AC=![]() b,
b,
∵CM∥BE,
∴![]() ,即
,即 ,
,
∴AE=3a,
∵∠OCN=∠ACM=∠ABE,
∴△ONC∽△AEB,
∴![]() ,即
,即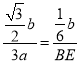 ,
,
解得:BE=![]()
∵AB2=AE2+BE2,即b2=![]() a2+9a2=
a2+9a2=![]() a2,
a2,
∵点A(a,![]() ),
),
则AB2=a2+![]()
解得:a2=3,则b=2![]() ,
,
故答案为2![]()


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.
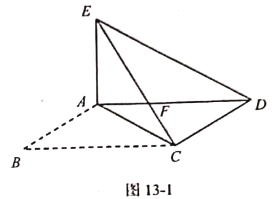
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
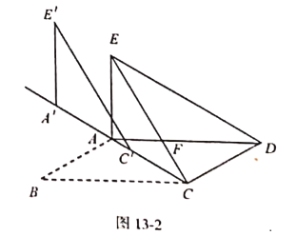
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴求该反比例函数和一次函数的解析式;
⑵在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标;
的坐标;
⑶直接写出当![]() 时,
时,![]() 的取值范围.
的取值范围.
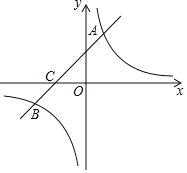
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在![]() 中,
中,![]() 把
把![]() 沿对角线
沿对角线![]() 所在的直线折叠,使点
所在的直线折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() .连接
.连接![]() .
.

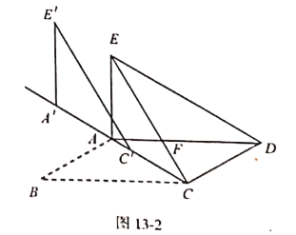
(1)求证:![]() ;
;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
(3)将图1中![]() 的沿射线
的沿射线![]() 方向平移得到
方向平移得到![]() (如图2所示) .若在
(如图2所示) .若在![]() 中,
中,![]() . 当
. 当![]() 时,直接写出
时,直接写出![]() 平移的距离.
平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
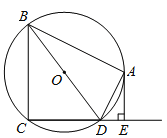
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
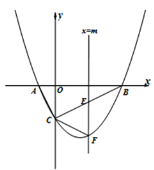
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=
与x轴交于A、B两点,与y轴交于点C,已知A(–1,0),且直线BC的解析式为y=![]() x-2,作垂直于x轴的直线
x-2,作垂直于x轴的直线![]() ,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
,与抛物线交于点F,与线段BC交于点E(不与点B和点C重合).
(1)求抛物线的解析式;
(2)若△CEF是以CE为腰的等腰三角形,求m的值;
(3)点P为y轴左侧抛物线上的一点,过点P作![]() 交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
交直线BC于点M,连接PB,若以P、M、B为顶点的三角形与△ABC相似,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四个命题:①如果一个数的相反数等于它本身,则这个数是0;②一个数的倒数等于它本身,则这个数是1;③一个数的算术平方根等于它本身,则这个数是1或0;④甲、乙两射击运动员分别射击10次,他们射击成绩的方差分别为![]() =5,
=5,![]() =2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=
=2,这一过程中乙发挥比甲更稳定.⑤点M(a,b),N(c,d)都在反比例函数y=![]() 的图象上.若a<c,则b>d.其中真命题有( )个.
的图象上.若a<c,则b>d.其中真命题有( )个.
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
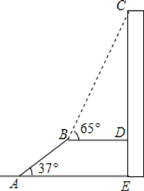
【题目】如图,AB是某火车站候车室前的自动扶梯,长为30m,坡角为37°,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度.(结果精确到0.1m)(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com