搜索
【题目】如图，阴影部分是边长是
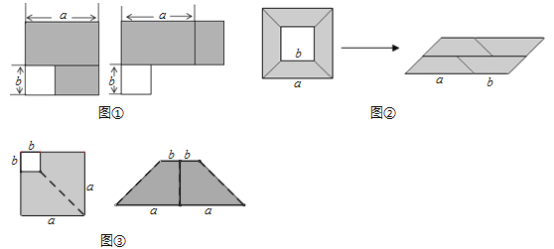
的大正方形剪去一个边长是
的小正方形后所得到的图形，将阴影部分通过割、拼，形成新的图形，给出下列3幅图割拼方法中，其中能够验证平方差公式有___________（填序号）
参考答案：
【答案】①②③
【解析】
分别在两个图形中表示出阴影部分的面积，继而可得出验证公式．
在图①中，左边的图形阴影部分的面积=a2-b2，右边图形中阴影部分的面积=（a+b）（a-b），故可得：a2-b2=（a+b）（a-b），可以验证平方差公式；
在图②中，阴影部分的面积相等，左边阴影部分的面积=a2-b2，右边阴影部分面积=（a+b）（a-b）．可得：a2-b2=（a+b）（a-b），可以验证平方差公式；
在图③中，阴影部分的面积相等，左边阴影部分的面积=a2-b2，右边阴影部分面积=
（2b+2a）（a-b）=（a+b）（a-b），可得：a2-b2=（a+b）（a-b），可以验证平方差公式.
故答案是：①②③
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线
与
轴交于点
（1，0）和点
，与
轴交于点
，对称轴为直线
＝1.（1）求点
的坐标（用含
的代数式表示）（2）连接
、
，若△
的面积为6，求此抛物线的解析式；（3）在（2）的条件下，点
为
轴正半轴上的一点，点
与点
，点
与点
关于点
成中心对称，当△
为直角三角形时，求点
的坐标.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程
（1）(x+3)(x﹣3)=3
（2）x2﹣2x﹣3=0(用配方法))；
（3）(x-5)2=2(5-x)
（4）6x2﹣x﹣2=0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为2的正方形ABCD中，点P是边AD上的动点（点P不与点A、点D重合），点Q是边CD上一点，联结PB、PQ，且∠PBC=∠BPQ．
（1）当QD=QC时，求∠ABP的正切值；
（2）设AP=x，CQ=y，求y关于x的函数解析式；
（3）联结BQ，在△PBQ中是否存在度数不变的角？若存在，指出这个角，并求出它的度数；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线
满足条件：（1）在
时， 
随
的增大而增大，在
时， 
随
的增大而减小；（2）与
轴有两个交点，且两个交点间的距离小于
.以下四个结论：①
；②
；③
；④
，说法正确的个数有（ ）个A. 4 B. 3 C. 2 D. 1
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线
交
轴于
点，交
轴于
点， 
为
的中点， 
为射线
上一点，连
，将
绕
点顺时针旋转
得线段
，则
的最小值为__________. -
科目： 来源： 题型：
查看答案和解析>>【题目】8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表(得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀)．
平均分
方差
中位数
众数
合格率
优秀率
一班
7.2
2.11
7
6
92.5%
20%
二班
6.85
4.28
8
8
85%
10%
根据图表信息，回答问题：
(1)用方差推断， 班的成绩波动较大；用优秀率和合格率推断， 班的阅读水平更好些；
(2)甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？
相关试题
