练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某商品现在售价为每件60元，每星期可卖出300件，市场调查反映：调整价格，每件涨价1元，每星期要少卖出10件；每件降价1元，每星期可多卖出20件.已知商品的进价为每件40元.

    （1）设每件降价x元，每星期的销售利润为y元；

    ① 请写出y与x之间的函数关系式；

    ② 确定x的值，使利润最大，并求出最大利润；

    （2）若涨价x元，则x= 元时，利润y的最大值为 元（直接写出答案，不必写过程）.

    【答案】（1）①②x=2或3时y最大为6120；（2）5， 6250

    【解析】试题分析：（1）①设每件降价x元，每星期的销售利润为y元，根据等量关系“总利润=每件的利润×每星期的销售量”，写出函数关系式即可；②把函数的解析式化为顶点式，然后根据x取整数，即可求得最大利润；（2）表示出商品的周销售量，根据等量关系“总利润=每件的利润×每星期的销售量”，写出函数关系式，再根据二次函数的性质求出最大利润即可.

    试题解析：

    （1）依题意得

    ①

    ∵,x为自然数 ∵

    故x=2或3时y最大为6120

    （2）x=5时，y最大为6250元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，P是A'B'的中点，连接PM．若BC＝2，∠BAC＝30°，则线段PM的最大值是（　　）

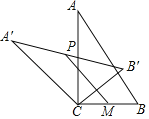
    A.4B.3C.2D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点O在线段AB上，AB=6，OC为射线，且∠BOC=45°．动P以每秒1个单位长度的速度从点O出发，沿射线OC做匀速运动．设运动时间为t 秒．

    （1）如图1，若AO=2．

    ①当 t=6秒时，则OP= ，S△ABP= ；

    ②当△ABP与△PBO相似时，求t的值；

    （2）如图2，若点O为线段AB的中点，当AP=AB时，过点A作AQ∥BP，并使得∠QOP=∠B，求AQBP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知直线交轴于点，交轴于点， 为的中点， 为射线上一点，连，将绕点顺时针旋转得线段，则的最小值为__________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB=BC=1，则下列结论：

    ①∠CAD=30°②BD=③S平行四边形ABCD=ABAC④OE=AD⑤S△APO=，正确的个数是（　　）

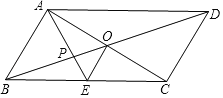
    A. 2 B. 3 C. 4 D. 5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

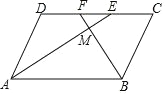
    【题目】如图，在 ABCD 中，AE、BF 分别平分∠DAB 和∠ABC，交 CD 于点 E、F，AE、BF 相交于点 M．

    （1）求证：AE⊥BF；

    （2）判断线段 DF 与 CE 的大小关系，并予以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】码头工人往一艘轮船上装载货物，装完货物所需时间 y(分钟)与装载速度 x(吨/分钟)之间的函数关系如图．

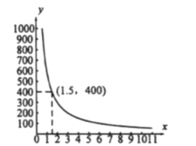
    （1）求y与x之间的函数表达式：

    （2）若要求在2小时至2.5小时内（包括2小时与2.5小时）装完这批货物，求装货速度的范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“不览夜景，味道重庆．”乘游船也有两江，犹如在星河中畅游，是一个近距离认识重庆的最佳窗口．“两江号”游轮经过核算，每位游客的接待成本为30元．根据市场调查，同一时段里，票价为40元时，每晚将售出船票600张，而票价每涨1元，就会少售出10张船票．

    （1）若该游轮每晚获得10000元利润的同时，适当控制游客人数，保持应有的服务水准，则票价应定为多少元？

    （2）春节期间，工商管理部门规定游轮船票单价不能低于44元，同时该游轮为提高市场占有率，决定每晚售出船票数量不少于540张，则票价应定为多少元，才能使每晚获得的利润最多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠AOB，以O为圆心，以任意长为半径作弧，分别交OA，OB于F，E两点，再分别以E，F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P，作射线OP，过点F作FD∥OB交OP于点D.

    (1)若∠OFD＝116°，求∠DOB的度数；

    (2)若FM⊥OD，垂足为M，求证：△FMO≌△FMD.

    查看答案和解析>>

    同步练习册答案