
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图:
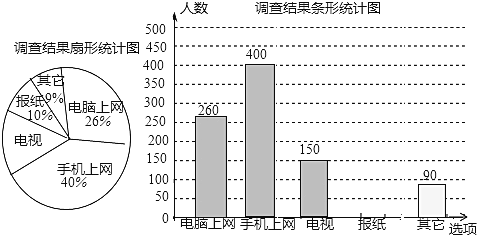
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是______;
(2)扇形统计图中,“电视”所对应的圆心角的度数是______;
(3)请补全条形统计图.
 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
的图像经过点M(-1,3)、N(1,5)。直线MN与坐标轴相交于点A、B两点.
(1)求一次函数的解析式.
(2)如图,点C与点B关于x轴对称,点D在线段OA上,连结BD,把线段BD顺时针方向旋转90°得到线段DE,作直线CE交x轴于点F,求![]() 的值.
的值.
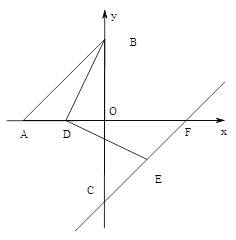
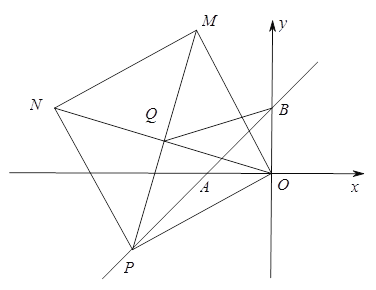
(3)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化,若不变,请求出其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
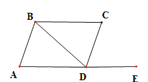
A.∠C=∠CDEB.∠ABD=∠CBDC.∠ABD=∠CDBD.∠C+∠ADC=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,△EFP的顶点E、F、P分别在线段AB、AD、AC上,且EP=FP.
(1)证明:∠EPF+∠BAD=180°.
(2)若∠BAD=120°(如图2),证明:AE+AF=AP.
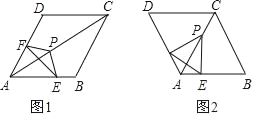
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
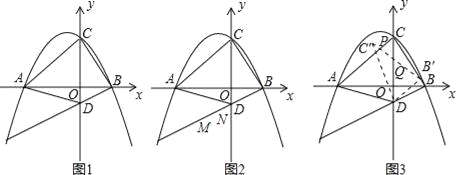
(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在数轴上对应的数为x,点B对应的数为y,且点O为数轴上的原点,且![]() .
.
![]()
(1)点A对应的数为______;点B对应的数为______;线段![]() 的长度为_______;
的长度为_______;
(2)若数轴上有一点C,且![]() ,求点C在数轴上对应的数;
,求点C在数轴上对应的数;
(3)若点P从A点出发沿数轴的正方向以每秒2个单位的速度运动,同时Q点从B点出发沿数轴的负方向以每秒4个单位长度的速度运动,运动时间为t秒,当![]() 时,求t的值.
时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为四家超市,其中超市D距A,B,C三家超市的路程分别为25km,10km,5km.现计划在A,D之间的道路上建一个配货中心P,为避免交通拥堵,配货中心与超市之间的距离不少于2km.假设一辆货车每天从P出发为这四家超市送货各1次,由于货车每次仅能给一家超市送货,因此每次送货后均要返回配货中心P,重新装货后再前往其他超市.设P到A的路程为xkm,这辆货车每天行驶的路程为ykm.
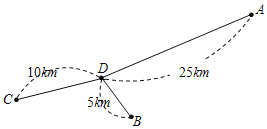
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)直接写出配货中心P建在什么位置,这辆货车每天行驶的路程最短?最短路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com