
【题目】如图1,菱形ABCD中,△EFP的顶点E、F、P分别在线段AB、AD、AC上,且EP=FP.
(1)证明:∠EPF+∠BAD=180°.
(2)若∠BAD=120°(如图2),证明:AE+AF=AP.
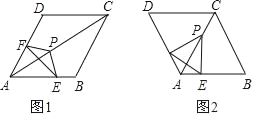
【答案】(1)证明见解析(2)证明见解析
【解析】分析:(1)如图1中,作PM⊥AD于M,PN⊥AC于N.由Rt△PMF≌Rt△PNE,推出∠MPF=∠NPE,推出∠EPF=∠MPF,由∠BAD+∠MPN=360°-∠AMP-∠ANP=180°,推出∠EPF+∠BAD=180°即可;
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.由Rt△PMF≌Rt△PNE,推出FM=NE,由PA=PA,PM=PN,推出Rt△PAM≌Rt△PAN,推出AM=AN,推出AF+AE=(AM+FM)+(AN-EN)=2AM,再证明PA=2AM即可解决问题;
详解:(1)如图1中,作PM⊥AD于M,PN⊥AC于N.

∵四边形ABCD是菱形,
∴∠PAM=∠PAN,
∴PM=PN,
∵PE=PF,
∴Rt△PMF≌Rt△PNE,
∴∠MPF=∠NPE,
∴∠EPF=∠MPF,
∵∠BAD+∠MPN=360°﹣∠AMP﹣∠ANP=180°,
∴∠EPF+∠BAD=180°.
(2)如图2中,作PM⊥AD于M,PN⊥AC于N.

由(1)可知Rt△PMF≌Rt△PNE,
∴FM=NE,
∵PA=PA,PM=PN,
∴Rt△PAM≌Rt△PAN,
∴AM=AN,
∴AF+AE=(AM+FM)+(AN﹣EN)=2AM,
∵∠BAD=120°,
∴∠PAM=60°,易知PA=2AM,
∴AE+AF=PA.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,OD平分∠BOC,OE平分∠AOC.
(1)若∠BOC=60°,∠AOC=40°,求∠DOE的度数;
(2)若∠DOE=n°,求∠AOB的度数;
(3)若∠DOE+∠AOB=180°,求∠AOB与∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD和菱形AEFG开始完全重合,现将菱形AEFG绕点A顺时针旋转,设旋转角∠BAE=α(0°<α<360°),则当α=_____时,菱形的顶点F会落在菱形ABCD的对角线所在的直线上.
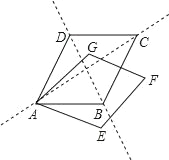
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD外一点,且DE=CE=![]() ,连接AE.
,连接AE.
(1)将△ADE绕点D逆时针旋转90°,作出旋转后的图形.
(2)如果∠AED=15°,判断△DEC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图:
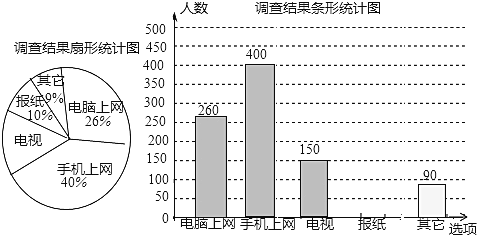
根据以上信息解答下列问题:
(1)这次接受调查的市民总人数是______;
(2)扇形统计图中,“电视”所对应的圆心角的度数是______;
(3)请补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.
(1)每副乒乓球拍和羽毛球拍的单价各是多少元?
(2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【探索发现】
如图①,是一张直角三角形纸片,∠B=60°,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
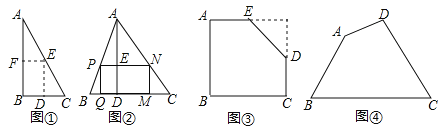
【拓展应用】
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
【灵活应用】
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),求该矩形的面积.
【实际应用】
如图④,现有一块四边形的木板余料ABCD,经测量AB=50cm,BC=108cm,CD=60cm,且tanB=tanC=![]() ,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com