
【题目】如图,E是正方形ABCD外一点,且DE=CE=![]() ,连接AE.
,连接AE.
(1)将△ADE绕点D逆时针旋转90°,作出旋转后的图形.
(2)如果∠AED=15°,判断△DEC的形状,并说明理由.

【答案】(1)见解析(2)△DEC是等边三角
【解析】分析:(1)根据旋转变换的定义和性质即可作图;
(2)先利用旋转性质知△DEF为等腰直角三角形,继而得出∠CFE=30°、∠AEF=60°、∠EGF=90°,从而求得EF=2、GE=1、CG=GE,据此知∠CEG=45°,根据∠CED=∠CEG+∠AED=60°、CE=DE即可得证.
详解:(1)如图所示,△CDF即为所求;

(2)△DEC是等边三角形,
理由:如图,连接EF,记AE、CF的交点为G,
由(1)可得DF=DE、∠EDF=90°、∠CFD=∠AED=15°,
∴∠DFE=∠DEF=45°,
∴∠CFE=∠DFE﹣∠CFD=30°,∠AEF=∠AED+∠DEF=60°,
∴∠EGF=90°,
∴GE=![]() EF,
EF,
∵EF=![]() =2,
=2,
∴GE=1,
∴CG=![]() =1,
=1,
∴CG=EG,
∵∠CGE=90°,
∴∠CEG=45°,
∴∠CED=∠CEG+∠AED=60°,
∵CE=DE,
∴△DEC为等边三角形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上任意两点之间的距离均可用“右﹣左”表示,即右边的数(较大)减去左边的数(较小).已知数轴上两点A、B对应的数分别为﹣2、5,则A、B两点之间的距离记为AB,且AB=5﹣(﹣2)=7.P为数轴上的动点,其对应的数为x.
![]()
(1)若点P到A,B两点的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到A,B两点的距离之和为11,若存在,请求出x的值;若不存在,请说明理由;
(3)若点P在原点,现在A,B,P三个点均向左匀速运动,其中点P的速度为每秒1个单位;A,B两点中有一个点速度与点P的速度一致,另一个点以每秒3单位的速度运动;则几秒后点P到A,B两点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=![]() BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,△EFP的顶点E、F、P分别在线段AB、AD、AC上,且EP=FP.
(1)证明:∠EPF+∠BAD=180°.
(2)若∠BAD=120°(如图2),证明:AE+AF=AP.
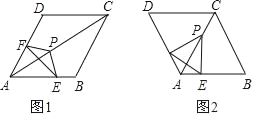
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题:
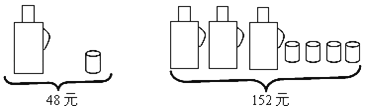
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和n(n>10,且n为整数)个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 从
从![]() 点出发沿
点出发沿![]() 的路线移动到点
的路线移动到点![]() 时停止,出发时以
时停止,出发时以![]() 单位/秒匀速运动:同时点
单位/秒匀速运动:同时点![]() 从
从![]() 出发沿
出发沿![]() 的路线匀速运动,移动到点
的路线匀速运动,移动到点![]() 时停止,出发时以
时停止,出发时以![]() 单位/秒运动,两点相遇后点
单位/秒运动,两点相遇后点![]() 运动速度变为
运动速度变为![]() 单位/秒运动,点
单位/秒运动,点![]() 运动速度变为
运动速度变为![]() 单位/秒运动:图2是射线
单位/秒运动:图2是射线![]() 随
随![]() 点运动在正方形
点运动在正方形![]() 中扫过的图形的面积
中扫过的图形的面积![]() 与时间
与时间![]() 的函数图象,图3是射线
的函数图象,图3是射线![]() 随
随![]() 点运动在正方形
点运动在正方形![]() 中扫过的图形的面积
中扫过的图形的面积![]() 与时间
与时间![]() 的图数图象,
的图数图象,
(1)正方形![]() 的边长是______.
的边长是______.
(2)求![]() ,
,![]() 相遇后
相遇后![]() 在正方形中所夹图形面积
在正方形中所夹图形面积![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
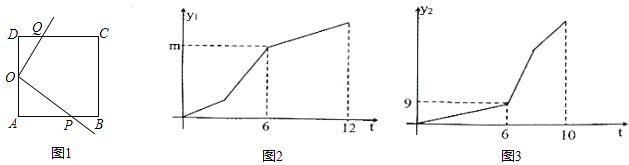
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com