
����Ŀ����ͼ1��������![]() �У�
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() �������
�������![]() ��·���ƶ�����
��·���ƶ�����![]() ʱֹͣ������ʱ��
ʱֹͣ������ʱ��![]() ��λ/�������˶���ͬʱ��
��λ/�������˶���ͬʱ��![]() ��
��![]() ������
������![]() ��·�������˶����ƶ�����
��·�������˶����ƶ�����![]() ʱֹͣ������ʱ��
ʱֹͣ������ʱ��![]() ��λ/���˶�,�����������
��λ/���˶�,�����������![]() �˶��ٶȱ�Ϊ
�˶��ٶȱ�Ϊ![]() ��λ/���˶�����
��λ/���˶�����![]() �˶��ٶȱ�Ϊ
�˶��ٶȱ�Ϊ![]() ��λ/���˶���ͼ2������
��λ/���˶���ͼ2������![]() ��
��![]() ���˶���������
���˶���������![]() ��ɨ����ͼ�ε����
��ɨ����ͼ�ε����![]() ��ʱ��
��ʱ��![]() �ĺ���ͼ��ͼ3������
�ĺ���ͼ��ͼ3������![]() ��
��![]() ���˶���������
���˶���������![]() ��ɨ����ͼ�ε����
��ɨ����ͼ�ε����![]() ��ʱ��
��ʱ��![]() ��ͼ��ͼ��
��ͼ��ͼ��
��1��������![]() �ı߳���______.
�ı߳���______.
��2����![]() ��
��![]() ������
������![]() ��������������ͼ�����
��������������ͼ�����![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
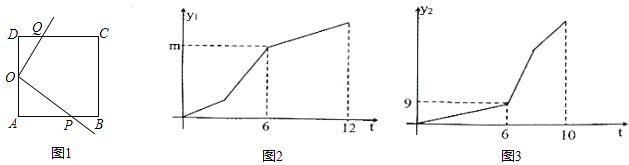
���𰸡���1��6����2�������.
��������
��1����ͼ3�п��Կ�������OQǰ��6��ɨ�������Ϊ9������Եõ�![]() ��
��![]() ADAD=9���Ӷ��ⷽ�̣���������εı߳�.
ADAD=9���Ӷ��ⷽ�̣���������εı߳�.
��2����ϸ�۲캯��ͼ���֪��P��Q���ڵ�C�����������ɣ�1���еõ��������α߳�����ã�����ǰ��P,Q���ٶȣ��ٻ���ͼ���г�ʽ����⼴��.
��:(1)��ͼ3��֪��OCD�����=9.
��O��AD���е㣬
��OD=![]() AD.
AD.
���ı���ABCD�������Σ�
��AD=CD����ODC=90�㣬
��![]() AD
AD![]() AD=9
AD=9
���:AD=6.
�ʴ�Ϊ6.
��2���۲�ͼ2��ͼ3��֪P��Q�������ڵ�C��������������ǰP��Q���ٶȷֱ�Ϊ2��1.������P,Q���˶��ٶȷֱ�Ϊ1��3.
�ٵ�6![]() t
t![]() ʱ����ͼ1��S=�����ε����-��POD�����-����OABQ�����.
ʱ����ͼ1��S=�����ε����-��POD�����-����OABQ�����. 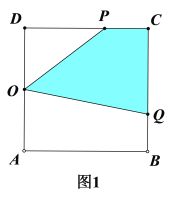
��PC=t-6,CQ=3(t-6)=3t-18.
��PD=12-t,BQ=24-3t.
��S=36-![]() (12-t)-3(3+24-3t)
(12-t)-3(3+24-3t)
=36-18+![]() t-81+9t
t-81+9t
=![]() t-63.
t-63.
�ڵ�8![]() t
t![]() 10ʱ����ͼ2��S=�����ε����-��POD�����-��AOQ�����.
10ʱ����ͼ2��S=�����ε����-��POD�����-��AOQ�����. 
��PC=t-6,BQ=3(t-8)=3t-24,
��PD=12-t,AQ=30-3t.
��S=36-![]() (12-t)-
(12-t)-![]() (30-3t)
(30-3t)
=36-18+![]() t-45+
t-45+![]() t.
t.
=6t-27.
��10<t![]() ʱ����ͼ3. S=�����ε����-��POD�����.
ʱ����ͼ3. S=�����ε����-��POD�����.
��PC=t-6, 
��PD=12-t,
��S=36-![]() (12-t)
(12-t)
=36-18+![]() t
t
=![]() t+18.
t+18.
����������![]() ��
��![]() ������
������![]() ��������������ͼ�����
��������������ͼ�����![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
��6![]() t
t![]() ʱS=
ʱS=![]() t-63����8
t-63����8![]() t
t![]() 10ʱ��S=6t-27����10<t
10ʱ��S=6t-27����10<t![]() ʱS=
ʱS=![]() t+18.
t+18.


 ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E��������ABCD��һ�㣬��DE=CE=![]() ������AE��
������AE��
��1������ADE�Ƶ�D��ʱ����ת90�㣬������ת���ͼ�Σ�
��2�������AED=15�����ж���DEC����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���������磬С���Ӽҳ����ܲ�ȥ�����ڹ�ͣ����һ����ؼң�ͼ�����߱� ʾС���뿪�ҵ�·��y���ף�������ʱ��x���֣�֮��ĺ�����ϵ��������˵���д�����ǣ� ��
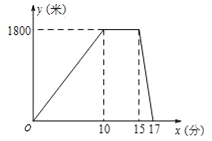
A��С���ڹ���Ϣ��5����
B��С���˳������17��
C��С���ܲ����ٶ�Ϊ180��/��
D�������ƽ���ٶ���900��/��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
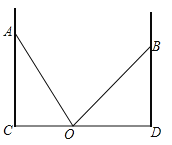
����Ŀ����֪��O��ֱ��AB�ϵ�һ�㣬��COE��90�㣬OF�ǡ�AOE��ƽ���ߣ�
(1)����C��E��F��ֱ��AB��ͬ��ʱ(��ͼ����ʾ)����˵����BOE��2��COF.
(2)����C���E��F��ֱ��AB������ʱ(��ͼ����ʾ)��(1)�еĽ����Ƿ���Ȼ�������������Ľ��ۣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
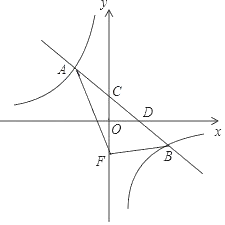
����Ŀ����ƽ��ֱ������ϵ�У�һ�κ���y����![]() x+b��ͼ���뷴��������y��
x+b��ͼ���뷴��������y��![]() ��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��k��0��ͼ����A��B���㣬��y�ύ�ڵ�C����x�ύ�ڵ�D������A������Ϊ����2��3����
��1����һ�κ����ͷ�������������ʽ��
��2��������C��y������ƽ��4����λ��������F������AF��BF�����ABF�������
��3������ͼ��ֱ��д������ʽ��![]() x+b��
x+b��![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ��п��������ԣ��ס��ҡ�����λͬѧ����������ѵ�������һ���˽������������һ���˽��£���ÿλ�����˴����������˵Ļ����Ǿ��ȵģ��ɼ�ʼ�����������Σ�
��1����������״ͼ�оٳ����δ�������п��������
��2�������δ������ص����µĸ��ʣ�
��3�����δ������ص����µĸ��ʴ��Ǵ����ҽ��µĸ��ʴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
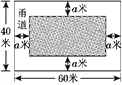
����Ŀ����ͼ����Ϊ����У������ijУ�ƻ���һ�鳤Ϊ60������Ϊ40�ij����οյ�������һ�������λ��������������������µĿյ�����ͬ���������������Ŀ�Ϊa����
 ��
�� ��
��
(1)�ú�a��ʽ�ӱ�ʾ���Ե������
(2)�������ռ��������������οյ������![]() �����ʱ���Ŀ���
�����ʱ���Ŀ���
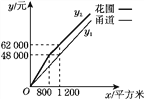
(3)��֪ij�ֹ�˾���������Ե����y1(Ԫ)��y2(Ԫ)�������x(ƽ����)֮��ĺ�����ϵ��ͼ����ʾ�����ѧУ�����ɸù�˾�н�����Ŀ����Ҫ����������������2���Ҳ�����10������ô���Ŀ�Ϊ������ʱ���������ͻ��Ե��������ͣ���������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣�ij��ѧ�����꼶��ȡ����ѧ�������������ԣ����涨��ÿ������90�����µ�Ϊ������ÿ������90��99�ε�Ϊ����ÿ������100��109�ε�Ϊ�еȣ�ÿ������110��119�ε�Ϊ���ã�ÿ������120�μ����ϵ�Ϊ���㣮���Խ���������Ƴ�����������������ͳ��ͼ�������ͼ����Ϣ��������и��⣺

��1���μ�����������ԵĹ��� �ˣ�
��2����ȫ����ͳ��ͼ��
��3��������ͳ��ͼ�У����е�����������Ӧ��Բ�ĽǵĶ����� ��
��4�������У�����꼶����������480�ˣ����ݴ�ͳ�����ݣ���������У�����꼶�����ɼ�Ϊ����������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AC��BDΪ��ֵ��ǽ�棬һ�����Ӵӵ�O���𣬵�����ǽ��AC��ʱ�����ӵ���һ�����ڵ�A������ʱ��AOC=60�㣬������ǽ��BD��ʱ�����ӵ���һ�����ڵ�B������ʱ��BOD=45�㣬��OD=3![]() �ף�
�ף�
��1�������ӵij�����2����OC��AC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com