练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】为了奖励优秀班集体,学校购买了若干副乒乓球拍和羽毛球拍,购买2副乒乓球拍和1副羽毛球拍共需116元,购买3幅乒乓球拍和2幅羽毛球拍共需204元.

    (1)每副乒乓球拍和羽毛球拍的单价各是多少元?

    (2)若学校购买5副乒乓球拍和3副羽毛球拍,一共应支出多少元?

    【答案】（1）一副乒乓球拍 28 元，一副羽毛球拍 60元（2）共 320 元．

    【解析】整体分析：

    （1）设购买一副乒乓球拍x元，一副羽毛球拍y元，根据“购买2副乒乓球拍和1副羽毛球拍共需116元，购买3幅乒乓球拍和2幅羽毛球拍共需204元”列方程组求解；（2）由（1）中求出的乒乓球拍和羽毛球拍的单价求解.

    解：（1）设购买一副乒乓球拍x元，一副羽毛球拍y元，

    由题意得，，

    解得：

    答：购买一副乒乓球拍28元，一副羽毛球拍60元.

    （2）5×28＋3×60＝320元

    答：购买5副乒乓球拍和3副羽毛球拍共320元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（10分）某体育用品专卖店销售7个篮球和9个排球的总利润为355元，销售10个篮球和20个排球的总利润为650元．

    （1）求每个篮球和每个排球的销售利润；

    （2）已知每个篮球的进价为200元，每个排球的进价为160元，若该专卖店计划用不超过17400元购进篮球和排球共100个，且要求篮球数量不少于排球数量的一半，请你为专卖店设计符合要求的进货方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG= ，则△CEF的周长为（ ）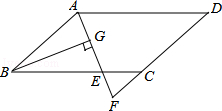
    A.8
    B.9.5
    C.10
    D.11.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正方形OABC的边长为2，顶点A，C分别在x轴的负半轴和y轴的正半轴上，M是BC的中点，P(0，m)是线段OC上一动点(C点除外)，直线PM交AB的延长线于点D.

    (1)求点D的坐标(用含m的代数式表示)；

    (2)当△APD是以AP为腰的等腰三角形时，求m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列说法不正确的是（ ）
    A.某种彩票中奖的概率是 ，买1000张该种彩票一定会中奖
    B.了解一批电视机的使用寿命适合用抽样调查
    C.若甲组数据的标准差S甲=0.31，乙组数据的标准差S乙=0.25，则乙组数据比甲组数据稳定
    D.在一个装有白球和绿球的袋中摸球，摸出黑球是不可能事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，放置的△OAB1 ， △B1A1B2 ， △B2A2B3 ， …都是边长为2的等边三角形，边AO在y轴上，点B1 ， B2 ， B3 ， …都在直线y= x上，则A2017的坐标为（ ）

    A.2015 ，2017
    B.2016 ，2018
    C.2017 ，2019
    D.2017 ，2017

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在杭州西湖风景游船处，如图，在离水面高度为5m的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13m，此人以0.5m/s的速度收绳.10s后船移动到点D的位置，问船向岸边移动了多少m？（假设绳子是直的，结果保留根号）

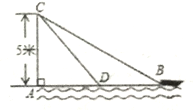
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市某风景区门票价格如图所示，黄冈赤壁旅游公司有甲、乙两个旅游团队，计划在“五一”小黄金周期间到该景点游玩．两团队游客人数之和为120人，乙团队人数不超过50人，设甲团队人数为x人．如果甲、乙两团队分别购买门票，两团队门票款之和为W元．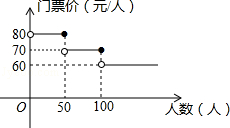
    （1）求W关于x的函数关系式，并写出自变量x的取值范围；
    （2）若甲团队人数不超过100人，请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱；
    （3）“五一”小黄金周之后，该风景区对门票价格作了如下调整：人数不超过50人时，门票价格不变；人数超过50人但不超过100人时，每张门票降价a元；人数超过100人时，每张门票降价2a元，在（2）的条件下，若甲、乙两个旅行团队“五一”小黄金周之后去游玩，甲乙两团队联合购票比分别购票最多节约3400元，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．
    （1）求证：直线BF是⊙O的切线；
    （2）若AB=5，sin∠CBF= ， 求BC和BF的长．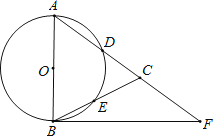

    查看答案和解析>>

    同步练习册答案