
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
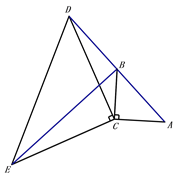
(1)求证:△ACD≌△BCE;
(2) 若AC=3cm,求BE的长度.
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .
.
例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=![]() .
.
⑴如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
⑵如果一个两位正整数t,t =10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为54,那么我们称这个数t为“吉祥数”,求所有的“吉祥数”;
⑶在⑵所得“吉祥数”中,求 F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.点P(3,﹣5)到x轴的距离为﹣5
B.在平面直角坐标系内,(﹣1,2)和(2,﹣1)表示同一个点
C.若x=0,则点P(x,y)在x轴上
D.在平面直角坐标系中,有且只有一个点既在x轴上,又在y轴上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l的解析式为y=![]() x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
(1)求出A点的坐标;
(2)若点 P在y轴上,且到直线l的距离为3,试求点P的坐标;
(3)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(4)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向y轴负半轴方向运动,求出点C运动中所有可能的时间t值,使得△ABC为轴对称图形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品因换季准备打折出售,如果按照原定价的七五折出售,每件将赔25元,而按原定价的九折出售,每件将赚20元,则这种商品的原定价是( )
A.200元B.300元C.320元D.360元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作三角形的类型:
尺 规 作 图 | 类型 | 依据 |
已知两边及其夹角作三角形 | __________ | |
已知两角一边作三角形 | __________(或 | |
已知三边作三角形 | __________ |
【答案】 SAS ASA SSS
【解析】试题解析:已知两边及其夹角作三角形,其依据是:SAS.
已知两角一边作三角形,其依据是:ASA(或![]() ).
).
已知三边作三角形, 其依据是: ![]()
故答案为: ![]()
点睛:判定三角形全等的方法有: ![]()
【题型】填空题
【结束】
11
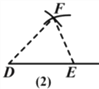
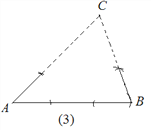
【题目】如图,根据图中作图痕迹,可以得出作三角形的依据分别是:
(1)__________;
(2)___________;
(3)__________.(图中虚线表示最后作出的线段)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,且OB=OC,下列结论:
①2b﹣c=2;②a=![]() ;③ac=b﹣1;④
;③ac=b﹣1;④![]() >0
>0
其中正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com