
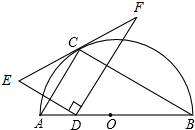
 如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点,
如图点C在以AB为直径的半圆的圆周上,若AB=4,∠ABC=30°,D为边AB上一动点,点E和D关于AC对称,当D与A重合时,F为EC的延长线上满足CF=EC的点,当D与A不重合时,F为EC的延长线与过D且垂直于DE的直线的交点,分析 (1)设DE交AC于M,DF交BC于N.由轴对称图形的性质可知EM=DM,ED⊥AC,然后可证明AC∥DF,由平行线分线成比例定理可知$\frac{CE}{CF}=\frac{EM}{MD}=1$;
(2)①当D与A不重合时.先证明四边形CNDM是矩形,从而得到MD∥BC,由平行线的性质可知∠ADM=∠ABC=30°,由特殊锐角三角函数可知ED=$\sqrt{3}x$,DN=$\frac{1}{2}BD$=$\frac{1}{2}×$(4-x)=2-$\frac{1}{2}x$,然后由平行线分线段成比例定理可知DN=NF,从而得到DF=2DN=4-x,最后在Rt△EFD中,由勾股定理可求得y与x的函数关系式;②当D与A重合时,y=2AC=4;
(3)①当点E在弧AC上时.由题意可知∠CAD=60°,由点E与点D关于AC对称可知:∠EAD=120°,故此点E不在弧AC上,故当且仅当点D与点A重合是,点E也与点A重合时,成立;②当点F在$\widehat{BC}$上时,如图3所示,连接BF、AF.由题意可知∠FDB=60°,由(2)可知DF=2DN,DB=2DN,故此DF=DB,从而可证明△DFB为等边三角形,于是得到DB=DF,然后再证明AD=DF,从而可知点D与点O重合,于是得到AD=$\frac{1}{2}AB$=2;
(4)由(2)可知∠EAD=2∠CAD=120°,故此点E运动的轨迹为一条线段,由(3)可知∠FBD=60°,故此点F运动的轨迹也是一条线段,然后画出图形,最后利用三角形的面积公式即可求得答案.
解答 解:(1)成立.
如图1所示:设DE交AC于M,DF交BC于N.
∵点E与点D关于AC对称,
∴EM=DM,ED⊥AC.
又∵DE⊥DF,
∴AC∥DF.
∴$\frac{CE}{CF}=\frac{EM}{MD}=1$.
∴CE=CF.
(2)①当D与A不重合时.
∵∠CMD=∠MDN=∠MCN=90°,
∴四边形CNDM是矩形.
∴MD∥BC.
∴∠ADM=∠ABC=30°.
∵在Rt△AMD中,∠ADM=30°,
∴MD=$\frac{\sqrt{3}}{2}AD$=$\frac{\sqrt{3}}{2}x$.
∴ED=$\sqrt{3}x$.
在Rt△BDN中,∠DBN=30°,
∴DN=$\frac{1}{2}BD$=$\frac{1}{2}×$(4-x)=2-$\frac{1}{2}x$.
∵MD∥BC,
∴$\frac{CF}{CE}=\frac{FN}{DN}=1$.
∴DN=NF.
∴DF=2DN=4-x.
在Rt△EDF中,由勾股定理可知EF=y=$\sqrt{E{D}^{2}+D{F}^{2}}$=$\sqrt{(\sqrt{3}x)^{2}+(4-x)^{2}}$=2$\sqrt{{x}^{2}-2x+4}$(0<x≤4);
②当D与A重合时,如图2所示;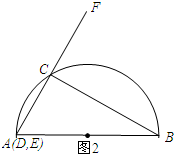
∵CF=EF,
∴y=2AC=4.
(3)①当点E在弧AC上时.
∵∠CAD=60°,点E与点D关于AC对称,
∴∠EAD=∠DAM=60°.
∴∠EAD=120°.
∵当点E在弧AC上时,∠EAD≤90°,
∴此种情况不成立.
故当且仅当点D与点A重合是,点E也与点A重合时,成立.
∴AD=0.
②当点F在$\widehat{BC}$上时,如图3所示,连接BF、AF.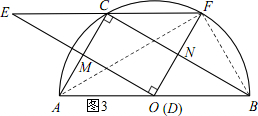
∵∠DBN=30°,∠BND=90°,
∴∠FDB=60°.
∵由(2)可知DF=2DN,DB=2DN,
∴DF=DB.
∴△DFB为等边三角形.
∴∠DBF=60°,∠DFB=60°.
∴∠AFD=30°.
∵AB是圆O的直径,
∴∠AFB=90°.
∵∠CFA=∠CBA=30°,
∴∠CFB=120°.
∴∠CFB+∠FBD=180°.
∴∠CF∥DB.
∴∠FAD=∠CFA=30°.
∴∠FAD=∠AFD=30°.
∴AD=DF=DB.
∴点D与点O重合.
∴AD=$\frac{1}{2}AB$=2.
综上所述,AD=0或AD=2.
(4)如图4所示;E、F的初始位置为E1、F1,E1与A点重合,E、F的终止位置为E2、F2,F2与B点重合.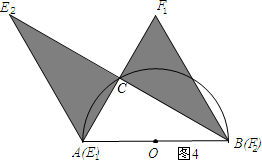
∵由(2)可知∠EAD=2∠CAD=120°,
∴点E运动的轨迹为线段AE1.
∵由(3)可知∠FBD=60°,
∴点F运动的轨迹为线段BF2.
∴阴影部分的面积即为所求,S=2×$\frac{1}{2}$×AC•BC=2×$\frac{1}{2}$×2$\sqrt{3}$×2=4$\sqrt{3}$.
点评 本题主要考查的是圆的综合应用,解答本题主要应用了轴对称图形的性质、平行线分线段成比例定理、等边三角形的性质和判定、等腰三角形的性质和判定,根据∠EAD和∠FBD为固定值,判断点E、F运动的轨迹都是一条线段是解题的关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{25}$=±5 | B. | 3$\sqrt{3}$-$\sqrt{27}$=1 | C. | $\sqrt{18}$×$\sqrt{2}$=6 | D. | $\sqrt{24}$×$\sqrt{\frac{2}{3}}$=$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知两个不平行的向量$\overrightarrow a,\overrightarrow b$.先化简,再求作:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$.
如图,已知两个不平行的向量$\overrightarrow a,\overrightarrow b$.先化简,再求作:$(\frac{1}{2}\overrightarrow a+3\overrightarrow b)-(\frac{3}{2}\overrightarrow a+\overrightarrow b)$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过4029或4030次移动后该点到原点的距离为2015个单位长度.
如图,某点从数轴上的A点出发,第1次向右移动1个单位长度至B点,第2次从B点向左移动2个单位长度至C点,第3次从C点向右移动3个单位长度至D点,第4次从D点向左移动4个单位长度至E点,…,依此类推,经过4029或4030次移动后该点到原点的距离为2015个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com