
在平面直角坐标系中,一次函数y=kx+b的图象与x轴、y轴分别相交于A(﹣3,0),B(0,﹣3)两点,二次函数y=x2+mx+n的图象经过点A.
(1)求一次函数y=kx+b的解析式;
(2)若二次函数y=x2+mx+n图象的顶点在直线AB上,求m,n的值;
(3)当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,求m,n的值.

(1)y=﹣x﹣3;(2)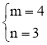 或
或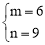 ;(3)m=2,n=﹣3.
;(3)m=2,n=﹣3.
【解析】
试题分析:(1)利用待定系数法求出解析式.
(2)根据二次函数的性质求出二次函数y=x2+mx+n图象的顶点,利用直线AB列出式子,再与点A在二次函数上得到的式子组成方程组求得m,n的值.
(3)分对称轴﹣3<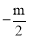 <0,
<0,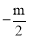 >0,
>0,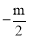 =0三种情况,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n,验证是否符合题意.
=0三种情况,结合二次函数y=x2+mx+n的图象经过点A得出的式子9﹣3m+n=0,求出m,n,验证是否符合题意.
试题解析:【解析】
(1)将A(﹣3,0),B(0,﹣3)代入y=kx+b得
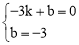 ,解得
,解得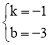 .
.
∴一次函数y=kx+b的解析式为:y=﹣x﹣3.
(2)二次函数y=x2+mx+n图象的顶点为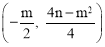 ,
,
∵顶点在直线AB上,∴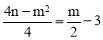 .
.
又∵二次函数y=x2+mx+n的图象经过点A(﹣3,0),∴9﹣3m+n=0.
∴二者联立,得 ,解得
,解得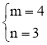 或
或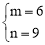 .
.
(3)∵二次函数y=x2+mx+n的图象经过点A,∴9﹣3m+n=0.
∵当﹣3≤x≤0时,二次函数y=x2+mx+n的最小值为﹣4,
∴①如答图1,当对称轴﹣3<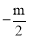 <0时,最小值为
<0时,最小值为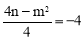 .
.
∴ ,解得
,解得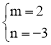 或
或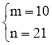 (由﹣3<
(由﹣3<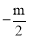 <0知不符合题意舍去).∴
<0知不符合题意舍去).∴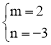 .
.
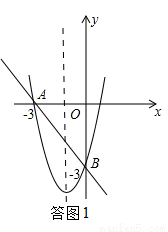
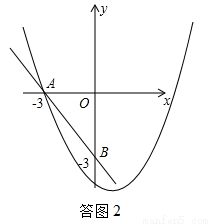
②如答图2,当对称轴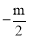 >0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
>0时,在﹣3≤x≤0时,x为0时有最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入与9﹣3m+n=0,得m=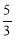 .
.
∵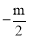 >0,∴m<﹣2. ∴此种情况不成立.
>0,∴m<﹣2. ∴此种情况不成立.
③当对称轴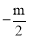 =0时,y=x2+mx+n的最小值为﹣4,
=0时,y=x2+mx+n的最小值为﹣4,
把(0,﹣4)代入y=x2+mx+n得n=﹣4,
把n=﹣4代入与9﹣3m+n=0,得m=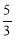 .
.
∵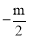 =0,∴m=0. ∴此种情况不成立.
=0,∴m=0. ∴此种情况不成立.
综上所述,m=2,n=﹣3.
考点:1.二次函数和一次函数综合题;2.曲线上点的坐标与方程的关系;3. 待定系数法的应用;4.二次函数的性质;5..分类思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(广西百色卷)数学(解析版) 题型:填空题
观察以下等式:32﹣12=8,52﹣12=24,72﹣12=48,92﹣12=80,…由以上规律可以得出第n个等式为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
如图1,在等腰梯形ABCD中,∠B=60°,P、Q同时从B出发,以每秒1单位长度分别沿B-A-D-C和B-C-D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平房单位),S与t的函数图象如图2所示,则下列结论错误的是( )

A.当t=4秒时,S=4
B.AD=4
C.当4≤t≤8时,S=2 t
t
D.当t=9秒时,BP平分梯形ABCD的面积
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西桂林卷)数学(解析版) 题型:选择题
在平面直角坐标系中,已知点A(2,3),则点A关于x轴的对称点坐标为( )
A.(3,2) B.(2, ) C.(
) C.( ,3) D.(
,3) D.( ,
, )
)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西崇左卷)数学(解析版) 题型:解答题
写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称:“等角对等边”).
已知:如图, .
求证: .
证明:

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西南宁卷)数学(解析版) 题型:解答题
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
(1) 求证:△ADE≌△CFE;
(2) 若GB=2,BC=4,BD=1,求AB的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(广西北海卷)数学(解析版) 题型:选择题
下列命题中,不正确的是( )
A.n边形的内角和等于(n﹣2)•180°
B.两组对边分别相等的四边形是矩形
C.垂直于弦的直径平分弦所对的两条弧
D.直角三角形斜边上的中线等于斜边的一半
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com