
已知抛物线 经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
经过A(2,0). 设顶点为点P,与x轴的另一交点为点B.
(1)求b的值,求出点P、点B的坐标;
(2)如图,在直线  上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
上是否存在点D,使四边形OPBD为平行四边形?若存在,求出点D的坐
标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,使△AMP≌△AMB?如果存在,试举例验证你的猜想;如果不存在,试说明理由.

(1) ,P的坐标为(4,
,P的坐标为(4, ),B的坐标是(6,0)(2)D点的坐标为(2,
),B的坐标是(6,0)(2)D点的坐标为(2,  )(3)存在,证明见解析
)(3)存在,证明见解析
【解析】解:(1)∵抛物线 经过A(2,0),
经过A(2,0),
∴ ,解得
,解得 。
。
∴抛物线的解析式为 。
。
∵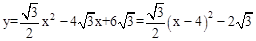 ,
,
∴顶点P的坐标为(4, )。
)。
令y=0,得 ,解得
,解得 。
。
∴点B的坐标是(6,0)。
(2)在直线  上存在点D,使四边形OPBD为平行四边形。理由如下:
上存在点D,使四边形OPBD为平行四边形。理由如下:
设直线PB的解析式为 ,把B(6,0),P(4,
,把B(6,0),P(4,  )分别代入,得
)分别代入,得
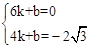 , 解得
, 解得 。
。
∴直线PB的解析式为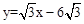 。
。
又∵直线OD的解析式为
∴直线PB∥OD。
设直线OP的解析式为 ,把P(4,
,把P(4,  )代入,得
)代入,得
 ,解得
,解得 。
。
如果OP∥BD,那么四边形OPBD为平行四边形。
设直线BD的解析式为 ,将B(6,0)代入,得
,将B(6,0)代入,得
 ,解得
,解得 。
。
∴直线BD的解析式为 。
。
联立方程组 ,解得
,解得 。
。
∴D点的坐标为(2,  )。
)。
(3)符合条件的点M存在。验证如下:
过点P作x轴的垂线,垂足为为C,
则PC= ,AC=2,
,AC=2,
由勾股定理,可得AP=4,PB=4。
又∵AB=4,∴△APB是等边三角形。
作∠PAB的平分线交抛物线于M点,连接PM,BM。
∵AM=AM,∠PAM=∠BAM,AB=AP,∴△AMP≌△AMB.(SAS)。
因此即存在这样的点M,使△AMP≌△AMB.。
(1)由抛物线 经过A(2,0),代入即可求出b的值;从而得出抛物线的解析式,化为顶点式即可求出顶点P的坐标;令y=0,即可求出点B的坐标。
经过A(2,0),代入即可求出b的值;从而得出抛物线的解析式,化为顶点式即可求出顶点P的坐标;令y=0,即可求出点B的坐标。
(2)用待定系数法,求出直线PB、BD的解析式,联立 和
和 ,解之即得点D的坐标。
,解之即得点D的坐标。
(3)由勾股定理求出AP、BP和AB的长,证出△APB是等边三角形,即可作BP的中垂线AM交BP于点M,点M即为所求。


科目:初中数学 来源: 题型:
 在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),
在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),查看答案和解析>>
科目:初中数学 来源: 题型:
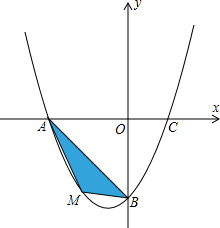
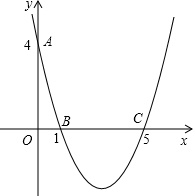 如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.
如图,在平面直角坐标系xoy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线对称轴l与x轴相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com