
【题目】如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
(1)请画出该蚂蚁沿长方体表面爬行的三条线路图(即平面展开图);
(2)已知蚂蚁沿长方体表面爬行的速度是1cm/s,问蚂蚁能否在8秒内获取到食物?

【答案】(1)图形见解析;(2)蚂蚁不能在8秒内获取到食物.
【解析】试题分析:
(1)按下图三种方式展开即可画出三条路线图;
(2)根据(1)中所画的路线图结合长方体的长、宽、高由勾股定理可计算出每条路线的长度,从而可得最短的路线长度,再除以蚂蚁爬行的速度即可得蚂蚁由A爬行到B所需的时间,与8比较即可得出结论.
试题解析:
(1)如下图所示:
从长方体的一条对角线的一个端点A出发,沿表面运动到另一个端点B,有以下三种方案:

(2)如图(1)由勾股定理得:AB= ![]()
如图(2)由勾股定理得:AB= ![]()
如图(3)由勾股定理得:AB= ![]()
∵![]() <
<![]() <
<![]()
∴它想吃到与顶点A相对的顶点B的食物最短路程为![]() ,
,
∴所需时间为![]()
∵![]()
∴![]()
∴ 蚂蚁不能在8秒内获取到食物.


科目:初中数学 来源: 题型:
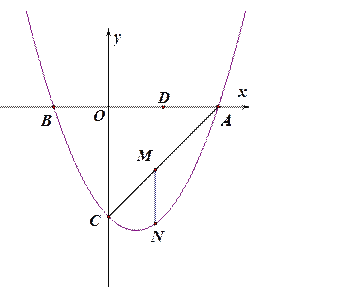
【题目】如图,抛物线![]() 与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于
与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于![]() 轴,交AC于点M.
轴,交AC于点M.
(1) 求直线AC的解析式;
(2)当点N运动至抛物线的顶点时,求此时MN的长;
(3)设点N的横坐标为t,MN的长度为l;
①求l与t之间的函数关系式,并写出t的取值范围;
②l是否存在最值,有如有写出最值;
(4)点D是点B关于![]() 轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
若存在,请求出此时△CAN的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P是∠MAN的角平分线上一点,PB⊥AM于B,PC⊥AN于C.
(1)如图1,点D、E分别在线段AB、AC上,且∠DPE=![]() ∠BPC,求证:DE=BD+CE;
∠BPC,求证:DE=BD+CE;

(2)如图2,若D在AB的延长线上,E在直线AC上,则DE、BD、CE三者的数量关系变化吗?若变化,请直接写出结论即可。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”是中国与世界的互利共赢之路,据统计,“一带一路”地区覆盖的总人口约为44亿人,则“44亿”这个数用科学记数法可表示为( )
A.4.4×107B.4.4×108C.4.4×109D.0.44×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com